课前准备
教师准备 多媒体课件
教学过程
⊙创设情境,导入教学
1.课件出示路线图。
2.师:这是老师上下班走的路线,从这幅路线图中你看到了什么?
生1:角。
生2:线。
生活中处处有数学,今天这节课,我们就来复习平面图形中有关线和角的知识。
(一)线的回顾学习。
1.回顾学过的线有哪几种。
(直线、射线、线段)
2.判断下面各是什么线。
(课件出示一组直线、射线和线段)
3.思考并交流:直线、射线、线段有什么区别?
| 直线 | 射线 | 线段 |
长度 | 无限 | 无限 | 有限 |
端点 | 无 | 1个 | 2个 |
与直线的关系 |
| 是直线的一部分 | 是直线的一部分 |
4.填一填。
(1)经过两点可以画( )条直线。
(2)两条直线相交,有( )个交点。
(以小组为单位,讨论、交流后完成)
5.追问:同一平面内两条直线有哪几种位置关系?
同一平面内两条直线的位置关系
6.指导学生完成教材91页“巩固与应用”1题。
7.讨论:什么叫互相垂直?什么叫互相平行?
(两条直线相交成直角时叫作互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫垂足;同一平面内不相交的两条直线叫作平行线,其中一条直线叫作另一条直线的平行线)
8.想一想,过一点怎样画已知直线的平行线和垂线?
预设
生1:画平行线:把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板和已知直线重合的直角边与已知点重合,过已知点沿三角板的直角边画直线即可。
生2:画垂线:用三角板的一条直角边与已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边与已知点重合,过已知点沿直角边向已知直线画直线即可。
(二)角的回顾学习。
1.说说你知道的角有哪些。
(锐角、直角、钝角、平角、周角)
(1)学生说角,教师出示角,并让学生说说角的度数或范围。
(2)完成教材90页4题。
2.究竟什么是角?谁能给它下个定义?
(由一点引出的两条射线所组成的图形叫作角)
3.角的大小与什么有关?
(角的大小与角的两边张开的程度有关,与两边的长短无关)
⊙典型例题解析
1.课件出示例1。
图中有多少条线段?多少条射线?多少条直线?
![]()
分析 线段有两个端点,以点A为端点,另一端是点B,C,D,可以得到三条线段,即AB,AC,AD;以点B为端点,另一端是点C,D,可以得到两条线段,即BC,BD;以点C为端点,另一端是点D,可以得到一条线段,即CD。
射线有一个端点,可以分别以点A,B,C,D为端点,向左数出4条,向右数出4条,共8条。
射线和线段是直线的一部分,所以只有一条直线。
解答 线段:3+2+1=6(条)
射线:4×2=8(条)
直线:1条
2.课件出示例2。
下面是一张长方形纸折叠起来后的图形,已知∠1=50°,求∠2的度数。
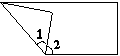
分析 将图形还原成长方形,如下图所示:
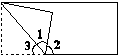
∠1与∠3的度数相等,即∠1+∠3=50°+50°=100°。因为∠1+∠2+∠3=180°,所以可以求出∠2的度数。
解答 (∠1+∠2+∠3)-(∠1+∠3)=180°-(50°+50°)=80°。
⊙探究活动
1.出示探究题。
A,B两镇位于河岸北侧,它们到河岸的距离如图所示。现要在岸边CD上建一水塔给两镇供水,水塔建在何处,才能使水管用料最省?
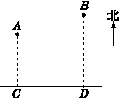
2.小组合作,先弄清本题考查的知识点是什么,再试做。(生做,师巡视,相机指导)
3.小组合作,汇报探究结果,说清解题思路。
生汇报后,教师明确:要使水管用料最省,必须在CD上找一点E,使AE与BE的和最小。因为两点之间线段最短,所以延长AC到点F,使AC=CF,连接BF,与CD相交于点E,EF=AE,这样在点E处建水塔,才能使水管用料最省。(图略)
4.小结。
此类问题要多动脑筋,结合图示和学过的知识进行解答。
⊙课堂总结
通过本节课的复习,你们有什么收获?
⊙布置作业
教材91页4题。
板书设计
线与角
直线 射线 线段
平行 相交
角
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |