|
(10)代数初步 (四)探索规律 

课前准备 教师准备 多媒体课件 教学过程 ⊙激趣引入 1.游戏引入:拍一下手,拍两下肩,拍三下腿,重复两次。你发现了什么? (板书课题:探索规律) 2.寻找生活中的数学规律。(全班交流,反馈订正) 师:找一找我们现在上课的教室里什么是有规律的。 生:座位排列有规律,电扇、电灯悬挂有规律……
师:老师今天有什么特别之处吗? 生:老师戴的项链上的珠子排列有规律。 师:你真棒,你有一双善于观察的眼睛。我相信你的这双眼睛一定会看到更精彩的世界。 师:生活中有规律的现象还有很多,今天我们就一起来研究“探索规律”。 ⊙探索规律 (一)完成乘法表,并找一找其中的规律。 1.填表。 师:请同学们把教材翻到87页,这张乘法表中有好多空白,你们能快速地把它补充完整吗? 2.交流。 师:谁来汇报一下你的结果? (抽查两行,课件显示) 3.根据填的结果,你能发现哪些数学规律? (教师根据学生的回答整理并归纳)
(1)横着看,每一行上的数都是第一个数的倍数。 (2)竖着看,每一列上的数都是下面第一个数的倍数。 (3)沿对角线斜着的一组数1,4,9,16,25,36,49,64,81分别是1,2,3,4,5,6,7,8,9的平方。
(二)填一填。(课件出示) 1.8,11,14,17,( ),23,( )。 2.4,9,16,25,( ),49,64。
3.1,8,27,( ),125,( )。 4.,,,,,。 学生独立完成后全班交流,得出如下规律: 1.相邻数之间相差3。 2.每个数都是平方数。 3.每个数都是立方数。 4.每个分数都相等。
(三)猜气球。 师:刚才我们找到的是数与数之间的规律,那么图形与图形之间会有什么规律呢?(课件出示教材87页2题) 师:你能说出第20个气球是什么颜色的吗?(学生找到图形之间的排列规律,小组交流得出第20个气球的颜色) 师:那第27个呢?(27÷5=5……2) (四)摆桌椅。
1.标准问题。 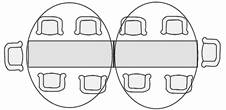
(1)1张桌子可坐6人,2张桌子可坐( )人,3张呢?4张呢? (2)猜想一下,10张桌子可坐多少人? (3)n张桌子呢?小组交流。 (4)小结:不管摆多少张桌子,我们都可以用4n+2表示可以坐的人数。 2.变式问题。
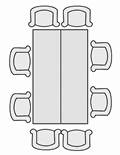
按照上图的摆法摆放桌子和椅子,完成下表。
小结:不管摆多少张桌子,我们都可以用2n+4表示可以坐的人数。 师:在桌子数相同时,哪种摆法可以坐的人数多?(小组交流) 3.探索问题。 如果由你负责这次的六一联欢会桌椅布置工作,你会选择哪种桌椅的摆法呢? ⊙典型例题解析 课件出示例题。 一些小球按下面的方式堆放。 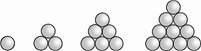 … …
(1) (2) (3) (4) 你知道第5堆有多少个小球吗?第8堆呢?
分析 本题探索的是图形中蕴涵的规律,通过依次观察每组图形可知,第一组图形有1个小球,第二组图形有(1+2)个小球,第三组图形有(1+2+3)个小球,第四组图形有(1+2+3+4)个小球,即第n组图形有(1+2+3+4+…+n)个小球。
解答 根据上面得出的规律可知,第5堆有1+2+3+4+5=15(个)小球,第8堆有1+2+3+4+5+6+7+8=36(个)小球。
|