设计说明 学生在前七册教材中,对整数四则运算已经有了较多的接触,积累了丰富的感性认识并掌握了相应的基础知识和技能。在此基础上对整数四则运算的意义和关系进行抽象、概括,小学阶段的抽象概括能力的培养需要借助一定的直观教学,因此,在设计本节课时,我注重借助线段图帮助学生直观形象地表达加、减法的意义,通过对比观察引导学生发现加、减法各部分间的关系。具体设计如下: 1.多角度提出问题,激发学习欲望。 提出一个问题比解决一百个问题更重要。《数学课程标准》强调培养学生发现问题、提出问题的能力。因此,在教学时,以教材创设的一列火车从西宁经过格尔木到达拉萨的路线图为背景,让学生根据图中的信息从不同角度提出数学问题,在感知数学问题来源于现实生活的同时,提升学生提出问题的能力,从而激发学生解决问题的欲望,使学生由原来被动的“要我学”转变为主动的“我要学”。 2.借助线段图,突出几何直观教学。 “几何直观”是《数学课程标准》提出的十个核心概念之一。它有助于学生理解题意,把复杂的问题简单化处理。因此,我将情境中的路线图抽象成线段图,在线段图中标明已知条件,这样既培养了学生几何直观的能力,又直观形象地表达了加、减法的意义。 3.对比观察,总结提升。 “推理、抽象、模型”思想是数学课程的三大核心数学思想。本环节通过让学生观察加、减法算式,进行对比,最终抽象、概括出加、减法的意义并发现加、减法各部分间的关系,从而建立数学模型。在这一过程中,学生不仅能获得成功的体验,更能增强学好数学的信心。
课前准备 教师准备 多媒体课件 课堂活动卡 学情检测卡 学生准备 直尺 注:本书“上课解决方案”中的“教学目标”“教学重难点”见前面的“备课解决方案”。 教学过程 ⊙创设情境,提出问题 1.出示示意图并提出问题。 同学们,今天老师给你们带来了我国的铁路路线图(课件出示铁路路线图),你们知道被称为“通往拉萨的天路”指的是哪一条铁路线吗?(青藏铁路)
2.标注数据并提出问题。(课件重点显示青藏铁路线,突出从西宁经格尔木到达拉萨这一段铁路线,并标注出西宁到格尔木的铁路长814 km,格尔木到拉萨的铁路长1142 km) 师:从图中你能获取哪些数学信息?你能根据获取的数学信息提出有价值的数学问题吗? 生1:我获取的数学信息是西宁到格尔木的铁路长814 km,格尔木到拉萨的铁路长1142 km。我提出的问题是西宁到拉萨的铁路长多少千米? 生2:知道总长和其中一部分的铁路长就可以求出剩下一部分的铁路长。 设计意图:引导学生观察铁路路线图,收集数学信息,并提出有价值的数学问题,在培养学生问题意识的同时,增进了数学与生活之间的联系,激发了学生的学习兴趣。 ⊙对比观察,探索新知 1.教学例1(1)。 (1)课件出示例1(1):一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长814 km,格尔木到拉萨的铁路长1142 km。西宁到拉萨的铁路长多少千米?
①指名读题,理解题意。(根据学生理解的题意,教师在黑板上用线段图表示出来) ②求西宁到拉萨的铁路长多少千米,应该怎样列式呢? 指名回答,教师板书:814+1142=1956(km)。 ③指名说一说算式中每个数表示的意义。(814表示西宁到格尔木的铁路长,1142表示格尔木到拉萨的铁路长,1956表示西宁到拉萨的铁路长) ④思考:加法的意义是什么呢? 组织学生先独立思考,再在小组中相互交流,然后指名汇报。 预设 生1:加法的意义就是把两部分合起来。 生2:加法的意义就是把两个数合起来。
(2)教师根据学生的汇报总结加法的意义。(把两个数合并成一个数的运算,叫做加法) (3)指出加法算式中各部分的名称。 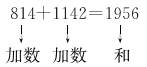
(相加的两个数叫做加数,加得的数叫做和) 2.教学例1(2)、(3)。 你们能根据算式814+1142=1956中的三个数提出用减法解决的问题吗? 预设 格尔木到拉萨的铁路长多少千米?西宁到格尔木的铁路长多少千米? (1)课件出示学生提出的问题。
西宁到拉萨的铁路长1956 km,其中西宁到格尔木的铁路长814 km。格尔木到拉萨的铁路长多少千米? 西宁到拉萨的铁路长1956 km,其中格尔木到拉萨的铁路长1142 km。西宁到格尔木的铁路长多少千米? (2)指名列式解答。 1956-814=1142(km) 1956-1142=814(km) (3)对比观察:与第(1)题相比,第(2)、(3)题分别是已知什么?求什么?怎样算? 组织学生先独立思考,再在小组中相互交流,然后指名汇报。
|