|
|
沙发

楼主 |
发表于 2012-4-5 20:14:31
|
只看该作者
【数论问题】
1.难度:★★★★
已知九位数2012□12□2既是9的倍数,又是11的倍数,那么,这个九位数是多少? 【答案】
设原数为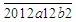 ,是9的倍数和11的倍数,那么一定是99的倍数。根据99的整除特征,两位一截后得到的两位数相加 ,是9的倍数和11的倍数,那么一定是99的倍数。根据99的整除特征,两位一截后得到的两位数相加 , ,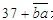 是99的倍数,只能是99,所以 是99的倍数,只能是99,所以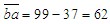 ,所以b=6,a=2。 ,所以b=6,a=2。
2.难度:★★★★★
四个连续自然数的乘积是11880,求此四个数。
【答案】
11880=2 ³×3 ³×5×11,把这些质因数搭配成4个乘数,并且要求是连续的,11比较大,我们不妨从11入手,只能有8,9,10,11或是9,10,11,12,前者不成立。那么这四个数是9,10,11,12。
|
|