
课前准备
教师准备 多媒体课件
学生准备 直尺 圆规 量角器
教学过程
⊙直接导入
师:条形统计图有哪些特点呢?
生:能直观看到项目的数量,便于比较。
师:上节课我们共同复习了条形统计图的相关知识,这节课我们一起来复习折线统计图和扇形统计图的知识。(板书课题:折线统计图和扇形统计图)
⊙回顾与整理
1.提问:上节课我们复习了条形统计图的特点、分类和绘制方法,这节课还是按照这三点来进行复习,下面请同学们分组讨论一下关于折线统计图和扇形统计图的相关知识。
2.教师出示讨论提纲,学生分组讨论。
讨论提纲:
(1)折线统计图和扇形统计图的特点。
(2)折线统计图的分类。
(3)折线统计图和扇形统计图的绘制方法。
3.充分讨论后汇报,教师在学生汇报的基础上小结。
(1)汇报统计图的特点。
①折线统计图的特点:不但可以表示数量的多少,还可以清楚地看出数量的增减变化情况。
②扇形统计图的特点:能清楚地看出各个部分量与总量之间的关系。
(2)折线统计图的分类:分为单式折线统计图和复式折线统计图。
(3)绘制方法。
折线统计图的绘制方法:
①整理数据。
②画出纵轴和横轴,用一个长度单位表示一定的数量。
③根据数据的多少描出各点,再把各点用线段顺次连接起来。
④写出统计图的名称和制图时间,并标出图例。
扇形统计图的绘制方法:
①根据所给的部分量和总量,求出各部分量占总量的百分比。
②用360°乘相应的百分比,得出扇形统计图中各个扇形所对应的圆心角的度数。
③画一个大小适当的圆,根据圆心角的度数画出对应的扇形。(注意各个扇形加起来必须是整圆)
④分别在各个扇形中标出对应部分的名称和百分比。
4.应用统计图的知识解决问题。
(1)课件出示统计表:光明路小学六年级共有45名学生,这个班2008~2013年拥有电话和电脑的家庭情况如下表:
年份 项目 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
电话/户 | 35 | 40 | 42 | 45 | 45 | 45 |
电脑/户 | 13 | 18 | 21 | 30 | 35 | 40 |
①请根据统计表中的数据绘制一幅折线统计图。
②拥有电话的户数哪两年增长幅度最大?
③拥有电脑的户数哪两年增长幅度最大?
④从统计数据中,你还发现了什么?
(2)学生明确题意,小组合作绘制折线统计图。(教师巡视,解决学生提出的问题)
(3)学生汇报自己的绘制方法,全班同学共同总结绘制统计图时需要注意的问题。
(4)小组探究,根据统计图回答问题。
5.三种统计图之间的联系与区别。
师生共同讨论比较,汇总。
名称 | 特点 | 作用 |
条形统 计图 | 用一个单位长度表示一定数量,用直条长短来表示数量的多少。 | 从图中能清楚地看出各种数量的多少,便于相互比较。 |
折线统 计图 | 用一个单位长度表示一定数量,用折线的上升或下降来表示数量的增减变化情况。 | 从图中能清楚地看出数量的增减变化情况,也能看出数量的多少。 |
扇形统 计图 | 用整个圆表示总量,用圆内的扇形表示各部分量占总量的百分比。 | 从图中能清楚地看出各部分量占总量的百分比,以及部分量与部分量之间的关系。 |
⊙典型例题解析
1.课件出示典型例题1。
六年级学生进行一次“我最喜欢的文艺节目”小调查,统计结果如下图。
六年级学生最喜欢的文艺节目情况统计图

(1)最喜欢小品节目的有60人,六年级学生有多少人?
(2)最喜欢歌曲节目的人数比喜欢相声节目的人数多多少人?
分析 (1)题考查的是扇形统计图的相关知识。从扇形统计图中可以知道最喜欢各种文艺节目人数的百分比,只有最喜欢小品节目的百分比没有给出。整个扇形表示单位“1”,用单位“1”减去各个百分比,即可求出最喜欢小品节目的人数占六年级总人数的百分比。因为最喜欢小品节目的有60人,所以六年级的总人数可求。
(2)题根据六年级的总人数和最喜欢歌曲节目人数占总人数的百分比,可以求出最喜欢歌曲节目的人数,用同样的方法可以求出最喜欢相声节目的人数,然后用最喜欢歌曲节目的人数减去最喜欢相声节目的人数,即最喜欢歌曲节目比最喜欢相声节目多出的人数。
解答 (1)60÷(1-15%-10%-25%-30%)=300(人)
答:六年级学生有300人。
(2)300×25%-300×10%=45(人)或300×(25%-10%)=45(人)
答:最喜欢歌曲节目的人数比最喜欢相声节目的人数多45人。
2.课件出示典型例题2。
李明和王亮是学校五年级数学组成员,现在要在两人中挑选一人去市里参加比赛,下图是他们四次选拔赛的成绩,选派( )更好。
李明和王亮数学选拔赛成绩统计图
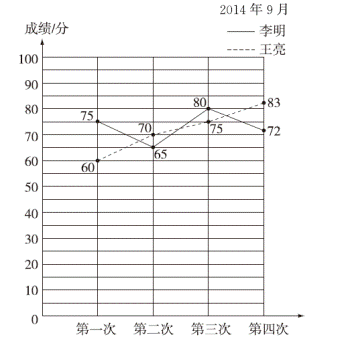
分析 从这幅统计图中可以看出李明的成绩不稳定,波动较大,而王亮的成绩呈逐渐上升的趋势,这说明王亮的潜力较大,以后成绩很有可能继续上升,所以让王亮去参加比赛更好。
解答 王亮
⊙探究活动
1.课件出示例题。
下面是一位病人的体温记录折线统计图,请看图填空。
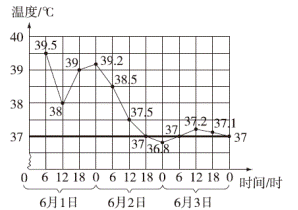
(1)护士每隔( )时给病人量一次体温。
(2)这位病人的体温最高是( )℃,最低是( )℃。
(3)他的体温在( )时至( )时下降最快;在( )这段时间比较稳定。
(4)图中的粗线表示( )。
(5)从体温上看,这位病人的病情在( )。(选填“好转”或“恶化”)
2.小组合作,讨论、分析、解答。
3.分析。
从折线统计图横轴的时间间隔上可以看出,统计的数据是每隔6时统计一次的,从6月1日0时到6月4日0时,共统计了12次。
折线的最高点对应的时间是6月1日6时,对应的体温是39.5℃,折线的最低点对应的时间是6月3日0时,对应的体温是36.8℃。
折线在6月1日6时至12时之间这部分的线段最陡,说明这段时间病人的体温下降最快。
在6月3日0时到6月4日0时之间,折线起伏变化不大,在37℃上下波动的幅度最大是0.2℃,说明这段时间比较稳定;图中的粗线对应的体温是恒定的,表示正常体温是37℃;从体温上看,病人的体温逐渐趋于平稳,恢复正常,说明他的病情在好转。
4.解答。
(1)护士每隔(6)时给病人量一次体温。
(2)这位病人的体温最高是(39.5)℃,最低是(36.8)℃。
(3)他的体温在(6月1日6)时至(6月1日12)时下降最快;在(6月3日0时至6月4日0时)这段时间比较稳定。
(4)图中的黑粗线表示(正常体温是37℃)。
(5)从体温上看,这位病人的病情在(好转)。(选填“好转”或“恶化”)
5.小结。
解决此类问题,要以统计图中的相关信息为依据,仔细观察,认真分析,联系生活实际,作出正确的判断。
⊙课堂总结
通过本节课的复习,我们知道了折线统计图和扇形统计图的特点和绘制方法。关于这两种统计图你还有哪些不明白的请提出来,我们来共同解决。(学生举手提问,师生共同解决学生的疑惑点)
⊙布置作业
1.教材103页2题。
2.教材104页5题。
板书设计
折线统计图和扇形统计图
折线统计图的特点:不但可以表示数量的多少,还可以清楚地看出数量的增减变化情况。
扇形统计图的特点:能清楚地看出各部分数量与总量之间的关系。
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |