

课前准备
教师准备 多媒体课件
教学过程
⊙系统整理,梳理脉络
用你自己的方法梳理学过的平面图形的相关知识,并找出它们之间的关系。(板书课题:平面图形)
图形


⊙回顾与整理
(一)复习三角形的相关知识。
1.提问:什么叫作三角形?你能画出几种不同的三角形?
课件出示三角形之间关系的集合图。
2.教师口述,学生作图。
(1)等腰三角形。
(2)等腰直角三角形。
(3)等边三角形。
(4)钝角三角形。
3.判断。
课件出示一组三角形,让学生说说各是什么三角形。
4.复习三角形的内角和。
提问:三角形的内角和是多少度?
学生交流并明确:三角形的内角和是180°。
5.三角形的边有什么性质?
明确:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
(二)复习四边形的相关知识。
提问:四边形是怎样的图形?我们曾经学习过哪些四边形?
预设
生:四边形是由四条线段首尾顺次相接围成的封闭图形,我们学过的四边形有长方形、正方形、平行四边形和梯形。
1.复习图形的特征。
课件出示:
![]()
请你说说上图中的四边形的名称和特征。
小组共同回忆:
(1)长方形有什么特征?
(2)正方形有什么特征?
(3)平行四边形有什么特征?
(4)梯形有什么特征?
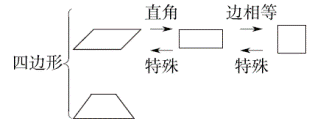
2.从图上看,我们学过的四边形可以分为哪几类?正方形、长方形和平行四边形之间有什么关系?为什么?
教师小结:因为长方形、正方形的两组对边分别平行,所以长方形、正方形是特殊的平行四边形,而正方形又是特殊的长方形。
教师根据各种四边形之间的关系逐步整理成下图。
(三)复习圆的相关知识。
师:刚才我们复习的图形都是直线图形。下面我们复习的图形是由曲线围成的,同学们能想出是什么图形吗?(圆)
师:先用圆规自己画一个圆,并用字母表示圆的圆心、半径和直径,然后完成下列问题。
1.同一个圆内的所有半径的长度都相等吗?
2.同一个圆内的半径和直径有什么关系?
3.圆的大小与什么有关?
4.在一个圆里有多少条半径?有多少条直径?
5.两端都在圆上的线段是直径吗?为什么?
(可以多让几名学生说一说,注意提问一些学习有困难的学生)
(四)复习轴对称图形的相关知识。
什么样的图形是轴对称图形?什么叫对称轴?我们学过的图形里,哪些是轴对称图形?
1.请同学们把圆对折并提问:你发现圆对折后有什么特点?再把等腰三角形、等边三角形对折,你们能发现什么?
2.提问:你认为刚才对折的图形都有什么特点?是什么图形?对折的折痕所在的直线是什么?等边三角形有多少条对称轴?圆有多少条对称轴?你还能说出哪些轴对称图形?
(五)举例说一说平面图形的特点在生活中的应用。
预设
生1:自行车车架是根据三角形具有稳定性的特点设计的。
生2:小区门口的电动推拉门是根据平行四边形易变形的特点设计的。
生3:盘子做成圆形的可以装更多的东西。
……
⊙典型例题解析
课件出示例题。
等腰三角形的一个内角是45°,其他两个内角各是多少度?
分析 本题考查的是等腰三角形的特点及三角形的内角和等知识。
假设45°是等腰三角形两个底角中的一个,则另一个底角也为45°,顶角为180°-45°×2=90°。
假设45°是等腰三角形的顶角,则两个底角均为(180°-45°)÷2=67.5°。
解答 45°为等腰三角形的一个底角,顶角为180°-45°×2=90°,另一个底角为45°;45°为等腰三角形的顶角,两个底角均为(180°-45°)÷2=67.5°。
⊙探究活动
1.出示探究题。
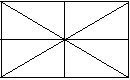
下图中有多少个长方形?多少个三角形?多少个梯形?
2.小组合作,明确分工,各自数出一种图形的个数。
3.小组汇报探究结果,说清解题思路。
学生汇报后,教师明确:要使数出的每种图形的个数没有遗漏和重复,就要有序地数,比如数三角形的个数可以先数出小三角形的个数(8个),再数由两个小三角形组成的三角形的个数(4个),然后数由4个小三角形组成的三角形的个数(4个),最后再相加(共16个)。其他图形的个数也要按照这种方法来数。
4.解答。
图中有9个长方形,16个三角形,8个梯形。
5.小结。
在数组合图形的个数时,要有序地数,这样才能做到不重复,不遗漏。
⊙课堂总结
在我们的日常生活中有许多数学问题,我们要善于发现问题之间的联系,多想想为什么,这样你也会收获解决问题的快乐。
⊙布置作业
教材91页2,3题。
板书设计
平面图形
平面图形
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |