课前准备
教师准备 多媒体课件
学生准备 准备圆的周长公式的推导过程图
教学过程
⊙创设情境,导入新知
师:请同学们认真观察一下,在我们的教室里面能找到哪些图形?
生:门是长方形的,灯的开关是正方形的,钟面是圆形的……
(教师根据学生的回答逐一将长方形、正方形、圆、三角形、梯形、平行四边形等平面图形贴到黑板上)
师:这些图形都是我们学过的什么图形?
生:平面图形。
师:今天我们就来共同复习关于平面图形周长的相关知识。(板书:平面图形的周长)
⊙小组合作,探究新知
1.什么是平面图形的周长?
(1)围成一个图形的所有边长的总和叫作这个图形的周长。
(2)封闭图形一周的长度叫作这个图形的周长。
2.你会计算哪些图形的周长?你是如何推导出这些图形的周长公式的?
(1)长方形的周长。
长方形的周长=(长+宽)×2,用字母表示为C=2(a+b)。
(2)正方形的周长。
正方形是特殊的长方形,正方形的周长=边长×4,用字母表示为C=4a。
(3)圆的周长。
因为圆的周长与直径的比值叫作圆周率,所以圆的周长=圆周率×直径,用字母表示为C=πd。
(结合学生的回答,课件演示各平面图形的周长公式的推导过程,并在相关的图形下板书字母公式)
(4)小结。
名称 | 长方形 | 正方形 | 平行四边形 | 梯形 | 三角形 | 圆 | |
周长公式 | 文字公式 | 长方形的周长=(长+宽)×2 | 正方形的周长=边长×4 | 平行四边形的周长=4条边长的和 | 梯形的周长=上、下两底长的和+两腰长的和 | 三角形的周长=3条边长的和 | 圆的周长=圆周率×直径(或圆周率×半 径×2)
|
字母公式 | C=2(a+b) | C=4a |
|
|
| C=πd或C=2πr | |
3.提问:平行四边形、梯形和三角形没有周长公式,我们怎么求周长?
预设
可以根据周长的意义,把图形的所有边长加起来,就是这个图形的周长。
4.完成教材94页6题。
5.长度单位及其进率。
提问:常用的长度单位有哪些?它们之间的进率分别是多少?
预设
生1:常用的长度单位有米、分米、厘米和毫米。
生2:1米等于10分米。
生3:1分米等于10厘米。
生4:1厘米等于10毫米。
生5:相邻的常用长度单位间的进率是10。
……
教师根据学生的回答板书,并让学生借助实例描述1米、1分米、1厘米和1毫米分别有多长。
⊙典型例题解析
1.课件出示例1。
一个半圆的半径是r,它的周长是( )。
A.πr B.πr+2r C.2πr D.2πr+2r
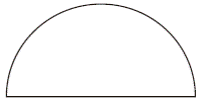
分析 此题容易给学生造成错觉,学生经常认为已知圆的半径,周长的计算公式就是C=2πr,则半圆的周长就是πr。这种想法是错误的,造成这种错误的原因是学生认为半圆的周长就是圆周长的一半,其实半圆的周长由两部分构成,即圆周长的一半和一条直径。如下图所示:

观察上图可知,圆周长的一半是πr,直径的长度是2r,所以半圆的周长是πr+2r。
解答 B
2.课件出示例2。
一辆自行车的车轮半径是40厘米,车轮每分转100圈,要通过2512米的桥,需要多少分?
分析 此题为行程问题中的求时间问题,根据行程问题的数量关系可知,时间=路程÷速度。
根据题意可知,自行车所行路程为2512米,所行速度没有直接给出,但是可以根据自行车车轮转动1圈的长度来求出车轮转动1分所走的路程(即速度)。
解答 自行车车轮转动1圈的长度:2×3.14×40÷100=2.512(米)
自行车的速度:2.512×100=251.2(米/分)
通过大桥的时间:2512÷251.2=10(分)
答:需要10分。
⊙探究活动
1.出示探究题。
张刚用绳子将底面半径是4厘米的4个圆柱捆绑在一起(如下图所示),你能求出一共需要多长的绳子吗?(接头处忽略不计)

2.小组讨论,探究解题思路及方法。
3.汇报解题方法。
预设
生1:通过观察可以看出,绳子的长度可以分成两部分,即直线部分和曲线部分。
生2:直线有4条,每条的长度是2条半径的长度和;曲线有4条,每条的长度是圆的长度,则4条曲线的长度是一个圆的周长。
生3:根据以上分析可以求出所用绳子的长度。
4条直线的长度:(4+4)×4=32(厘米)
4条曲线的长度:2×3.14×4=25.12(厘米)
绳子的长度:32+25.12=57.12(厘米)
4.活动小结。
解决此类问题的关键是要明确每条曲线和直线的长度分别是多少,然后将各自的长度相加就是所用绳子的总长度。
⊙课堂总结
通过本节课的学习,你有哪些收获?
⊙布置作业
教材95页5题。
板书设计
平面图形的周长
长方形的周长=(长+宽)×2,用字母表示为C=2(a+b)。
正方形的周长=边长×4,用字母表示为C=4a。
圆的周长=圆周率×直径,用字母表示为C=πd。
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |