课前准备
教师准备 多媒体课件
教学过程
⊙问题导入
师:谁能说一说什么是平面图形的面积?
生:物体的表面或围成的平面图形的大小,叫作它的面积。
师:这节课我们就来复习平面图形的面积的相关知识。(板书课题:平面图形的面积)
⊙回顾与整理
1.面积的计算公式。
(1)我们学习过哪些图形的面积的计算方法?
(长方形、正方形、平行四边形、三角形、梯形和圆)
结合学生的回答有序地画出相关平面图形,为构建知识网络作准备。
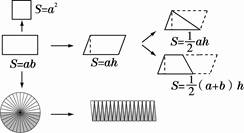
(2)如何计算这些平面图形的面积?各面积公式之间有什么联系?
①长方形的面积=长×宽,用字母表示为S=a×b。
②正方形是特殊的长方形,正方形的面积=边长×边长,用字母表示为S=a·a=a2。
③平行四边形的面积=底×高,用字母表示为S=a×h。
④三角形的面积=底×高÷2,用字母表示为S=ah。
⑤梯形的面积=(上底+下底)×高÷2,用字母表示为S=(a+b)h。
⑥圆的面积=圆周率×半径的平方,用字母表示为S=πr2。
(结合学生的回答,教师课件演示各个公式的推导过程,并在相关图形下板书字母公式)
⑦各面积公式之间的联系。

S=πr2
⑧列表总结平面图形的面积公式。
名称 | 长方形 | 正方形 | 平行四边形 | 梯形 | 三角形 | 圆 | |
面积公式 |
文字公式 | 长方形的面 积=长×宽 | 正方形的面积=边长×边长 | 平行四边形的面积=底×高 | 梯形的面积=(上底+下底)×高÷2 | 三角形的面积=底×高÷2 | 圆的面积=圆周率×半径的平方 |
字母公式 | S=ab | S=a2 | S=ah | S=(a+b)h | S=ah | S=πr2 | |
2.常用的面积单位及其进率。
(1)常用的面积单位有哪些?
(常用的面积单位有平方米、平方分米和平方厘米)
借助实例说一说1平方米,1平方分米,1平方厘米分别有多大。
(2)相邻的常用面积单位间的进率是多少?
(因为1平方米=100平方分米,1平方分米=100平方厘米,所以相邻的常用面积单位间的进率是100)
(3)面积单位间的互化。
①提问:如何把高级的面积单位化成低级的面积单位?如5.5平方米=( )平方分米。
②学生小组讨论后得出结论:把高级的面积单位化成低级的面积单位,要用它们之间的进率去乘高级单位的数。
上面的题目是把高级面积单位化成低级面积单位,平方米和平方分米之间的进率是100,所以5.5平方米=5.5×100=550平方分米。
③如果把低级的面积单位化成高级的面积单位,应该怎样做?
学生小组讨论后得出结论,并自行举例验证。
(4)公顷和平方千米。
预设
表示比较大的面积时,用到的面积单位还有公顷和平方千米。
生1:1平方千米=100公顷
生2:1公顷=10000平方米
生3:1平方千米=1000000平方米
⊙典型例题解析
1.课件出示例1。
(1)如下图,把一个长方形框架拉成一个平行四边形,这个平行四边形的面积与原来长方形的面积相比,( )。
![]()
A.长方形的面积大 B.平行四边形的面积大
C.面积一样大
(2)等腰梯形的周长是48厘米,面积是96平方厘米,高是8厘米,则腰长是( )。
A.24厘米 B.12厘米 C.18厘米 D.36厘米
问题(1)分析 本题考查学生对周长相等的长方形和平行四边形面积大小的掌握情况。
把一个长方形框架拉成一个平行四边形,周长没变,底边没变,但高变了,所以面积发生了变化,面积变小了。
解答 A
问题(2)分析 本题考查学生运用梯形的周长、面积等知识解答相关问题的能力。
梯形的面积=(上底+下底)×高÷2,(上底+下底)=梯形的面积×2÷高;
梯形的两腰和=梯形的周长-(上底+下底),腰长=梯形的两腰和÷2。
96×2÷8=24(厘米)
48-24=24(厘米)
24÷2=12(厘米)
解答 B
2.课件出示例2。
 计算这个图形的面积需要知道哪些条件?量一量,并算出图形
计算这个图形的面积需要知道哪些条件?量一量,并算出图形
的面积。
分析 本题考查学生对平行四边形高的测量方法、面积的计算方法的掌握情况。
计算这个图形的面积需要知道平行四边形的一个底以及该底上的高。
解答 测量并计算出面积。
⊙探究活动
1.出示探究题。

王大爷用篱笆围了一个半圆形的养鸡场。已知养鸡场的直径是12 m。篱笆长多少米?养鸡场的占地面积是多少平方米?
2.小组合作,分析、讨论、解答。
3.汇报解题思路、解法及注意事项。
预设
生1:求篱笆的长就是求半圆形养鸡场的周长。
从图上可以看出,半圆的周长应包括半圆的弧长和一条直径的长,所以篱笆的长是3.14×12÷2+12=30.84(m)。
生2:求养鸡场的占地面积就是求半圆的面积。半圆的面积就是圆面积的一半,所以养鸡场的占地面积是3.14×(12÷2)2÷2=56.52(m2)
4.小结。
从例题中我们发现,半圆的面积就是圆面积的一半,但半圆的周长并不等于圆周长的一半,类似的还有一个长方形分成两个相等的长方形之后,每个小长方形的面积等于大长方形面积的一半,但每个小长方形的周长不等于大长方形周长的一半;一个圆柱切成两段后,总体积没有变化,但总表面积却发生了变化。这些“变”与“不变”,都是值得我们思考和研究的。
⊙课堂总结
通过本节课的学习,你有哪些收获?
⊙布置作业
教材95页4题。
板书设计
平面图形的面积
![]()

S=ab S=a2
![]()
![]()
S=ah S=ah

![]()
S=πr2 S=(a+b)h
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |