课前准备
教师准备 多媒体课件
学生准备 100以内的数表
教学过程
⊙谈话引入,揭示目标
师:上节课我们把数进行了分类整理,这节课我们就一起来复习因数和倍数的相关知识。
⊙回顾与整理
1.回顾旧知,构建知识网络。
(1)回顾:因数和倍数这部分知识有哪些概念?
(因数、倍数、质数、合数、奇数、偶数等)
(2)讨论:各概念之间的关系是怎样的?
(组内交流)
(3)梳理:小组合作,用自己喜欢的方法进行知识梳理。
(4)汇报:各自的知识梳理方法。
(课件展示学生的梳理方法,肯定其优点后,引导其完善树状知识网络图)
2.复习、理解相关概念。
(1)因数和倍数。
①在数学上,关于“因数”和“倍数”是怎么定义的?
[整数A除以整数B(B≠0),除得的商是整数且没有余数,我们就说整数A能被整数B整除,或者说整数B能整除整数A。
如果整数A能被整数B(B≠0)整除,整数A就叫作整数B的倍数,整数B就叫作整数A的因数。倍数和因数是相互依存的。
如45能被9整除,所以45是9的倍数,9是45的因数]
师:为了方便,在研究因数和倍数时,所说的数指的是非零整数。
②举例说明因数和倍数各有什么特征。
预设
生1:一个数的因数的个数是有限的,其中最小的是1,最大的是它本身。如20的因数有1,2,4,5,10,20。共6个。
生2:一个数的倍数的个数是无限的,其中最小的是它本身,没有最大的倍数。如4的倍数有4,8,12,…
生3:一个数最大的因数等于它最小的倍数。
……
(2)质数与合数。
根据一个数所含因数的个数的不同,还可以得到质数与合数的概念。
①什么是质数?最小的质数是什么?
[一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数),最小的质数是2]
②什么是合数?最小的合数是什么?
(一个数,如果除了1和它本身还有别的因数,这样的数叫作合数,最小的合数是4)
(3)公因数和公倍数。
①什么叫公因数?什么叫最大公因数?
(几个数公有的因数,叫作这几个数的公因数。其中最大的一个叫作这几个数的最大公因数)
②什么叫公倍数?什么叫最小公倍数?请举例说明。
预设
生:几个数公有的倍数,叫作这几个数的公倍数,其中最小的一个,叫作这几个数的最小公倍数。如2的倍数有2,4,6,8,10,12,14,16,18,…3的倍数有3,6,9,12,15,18,…其中6,12,18,…是2和3的公倍数,6是它们的最小公倍数。
(4)探究2,5,3的倍数的特征以及奇偶数。
①2的倍数的特征是什么?什么是偶数?什么是奇数?举例说明。
预设
生1:个位上是0,2,4,6,8的数都是2的倍数。如58。
生2:是2的倍数的数叫作偶数。如20。
生3:不是2的倍数的数叫作奇数。如31。
②5的倍数的特征是什么?举例说明。
(个位上是0或5的数,都是5的倍数。如10,25,45,60等)
③3的倍数的特征是什么?举例说明。
(一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。如123,303等)
(5)复习质数、合数的判断方法及最小公倍数和最大公因数的求法等。
①如何判断一个数是质数还是合数?1是什么数?
(根据质数、合数的含义来判断。1既不是质数也不是合数)
②公因数与互质数的概念有什么联系?
(公因数只有1的两个数是互质数)
③互质数与质数有什么区别?
(互质数讲的是两个数之间的关系,这两个数的公因数只有1;质数是对一个自然数而言的,它只有1和它本身两个因数)
④求两个数的最大公因数和最小公倍数通常用什么方法。
(根据各自的定义或列举法)
(6)在100以内的数表中,用“○”圈出所有质数,用“__”画出7的倍数。
⊙典型例题解析
1.课件出示例1。
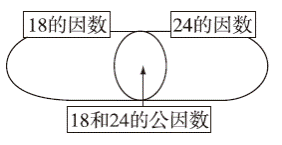
在下面的圈里填上适当的数。
(1) 
(2) 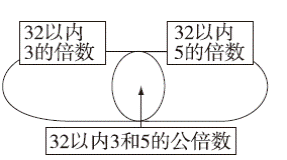
分析 本题考查的是因数、公因数、倍数、公倍数等知识。解题时先分别找到两个数各自的因数(或倍数),再找公有的因数(或倍数)。
(1)18的因数有1,2,3,6,9,18;
24的因数有1,2,3,4,6,8,12,24;
18和24的公因数有1,2,3,6。
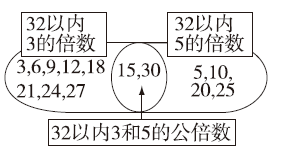
(2)32以内3的倍数有3,6,9,12,15,18,21,24,27,30;
32以内5的倍数有5,10,15,20,25,30;
32以内3和5的公倍数有15,30。
解答 (1) 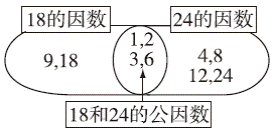
(2) 
2.课件出示例2。
一个长方体木块,长27厘米,宽18厘米,高15厘米。要把它切成大小相等的正方体木块,不许有剩余,正方体木块的棱长最大是多少厘米?
分析 本题考查的是灵活运用最大公因数的知识解决问题的能力。
根据题意,正方体木块的棱长最大应该是长方体木块长、宽、高的最大公因数。
解答 27的因数有1,3,9,27。
18的因数有1,2,3,6,9,18。
15的因数有1,3,5,15。
27,18,15的最大公因数是3,所以正方体木块的棱长最大是3厘米。
⊙探究活动
1.幼儿园有若干人排队做操,如果2人一行余1人,3人一行余2人,4人一行余3人,那么幼儿园排队做操的最少有多少人?
(1)明确探究要求。
讨论明确:
①这道题考查的是什么?
②怎样解决这个问题?
(2)汇报讨论结果。
预设
生1:这道题考查的是运用倍数知识解决问题的能力。
生2:2人一行余1人,说明总人数比2的倍数少1;3人一行余2人,说明总人数比3的倍数少1;4人一行余3人,说明总人数比4的倍数少1。
生3:根据题意,幼儿园排队做操的人数比2,3,4的最小公倍数少1人,所以先求出2,3,4的最小公倍数,再减1就可以了。
(3)尝试解答。
(关注学生求三个数的最小公倍数的情况,发现问题及时点拨)
(4)汇报解答过程。(指名板演,集体订正)
2的倍数有2,4,6,8,10,12,…
3的倍数有3,6,9,12,15,…
4的倍数有4,8,12,16,…
2,3,4的最小公倍数是12。
12-1=11(人)
答:幼儿园排队做操的最少有11人。
2.小结。
解答此类问题,关键要弄清考查的是因数知识还是倍数知识,同时要会求两个数或三个数的最大公因数及最小公倍数。
⊙课堂总结
通过本节课的复习,你有什么收获?
⊙布置作业
1.教材67页5题(3),(4)。
2.教材67页7题。
板书设计
因数和倍数
1.一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
2.一个数的倍数的个数是无限的,其中最小的因数是它本身,没有最大的倍数。
3.一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数),最小的质数是2。
4.一个数,如果除了1和它本身还有别的因数,这样的数叫作合数,最小的合数是4。
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |