
课前准备
教师准备 多媒体课件
教学过程
⊙谈话导入
我们学过哪些运算?这些运算的意义是什么?相关的知识都有哪些?这节课我们就来系统地归纳、整理四则运算的知识。
⊙回顾与整理
1.四则运算的意义。
(1)我们学过哪些运算?举例子说明。
生1:加、减、乘、除。
生2:列举算式……
(2)课件出示教材70页1题。
庆祝“六一”。

你能提出哪些数学问题?在解决问题的过程中,你用了哪些运算?
预设
生1:我根据第一幅图提出问题,两个同学一共折了多少只纸鹤?用加法计算,列式为26+39=65(只)。
生2:我根据第一幅图提出问题,还要折多少只纸鹤?用减法计算,列式为120-26-39=55(只)或120-(26+39)=55(只)。
生3:我根据第二幅图提出问题,一共需要多少钱?用乘法计算,列式为1.5×52=78(元)。
生4:我根据第三幅图提出问题,扎蝴蝶结用了多少米彩带?用乘法计算,列式为18×=9(m)。
生5:我根据第四幅图提出问题,平均每组有几名同学?用除法计算,列式为36÷4=9(名)。
(教师结合学生的提问、解答,用课件展示相关算式)
(3)结合上面的算式,完成下面的表格。
(注意引导学生考虑全面,结合学生的回答,用课件展示下表)
| 算 式 | 意 义 |
加法 | 26+39=65 | 把几个数合并成一个数的运算。 |
减法 | 120-26-39=55或120-(26+39)=55 | 已知两个数的和与其中的一个加数,求另一个加数的运算。 |
乘法 | 1.5×52=78 | 求几个相同加数的和的简便运算。 |
18×=9 | 求一个数的几分之几是多少。 | |
除法 | 36÷4=9 | 已知两个因数的积与其中的一个因数,求另一个因数的运算。 |
(4)整数、分数、小数运算的哪些意义相同?
预设
生1:整数、分数、小数的加法、减法、除法的意义相同。
生2:分数乘法的意义分两种情况,一种是求几个相同加数的和的简便运算,一种是求一个数的几分之几是多少。
2.四则运算的关系。
(1)陈述加与乘、加与减、乘与除相互间的关系。
预设
生1:加法是最基本的运算,整数乘法是求几个相同加数的和的简便运算。
生2:加法是把几个数合并成一个数的运算,而减法是知道总数和其中一部分,求另一部分,加法和减法是互逆关系,减法是加法的逆运算。
生3:乘法是求几个相同加数的和的简便运算,除法是把一个数进行平均分,求份数或每份数,乘法和除法是互逆关系,除法是乘法的逆运算。
(2)陈述加、减、乘、除算式中各部分之间的关系。
预设
生1:一个加数+另一个加数=和,一个加数=和-另一个加数。
生2:被减数-减数=差,被减数-差=减数,减数+差=被减数。
生3:一个因数×另一个因数=积,积÷一个因数=另一个因数。
生4:被除数÷除数=商,除数×商=被除数,被除数÷商=除数。
生5:被除数=除数×商+余数。
整理表格如下:
加法 | 减法 | 乘法 | 除法 |
一个加数+另一个加数=和 | 被减数-减数=差 | 一个因数×另一个因数=积 | 被除数÷除数=商 |
一个加数=和-另一个加数 | 被减数-差=减数 | 积÷一个因数=另一个因数 | 被除数÷商=除数 |
| 减数+差=被减数 |
| 除数×商=被除数 被除数=除数×商+余数 |
3.四则运算的应用。
举例说明生活中哪些地方会用到乘法运算,哪些地方会用到其他运算。
引导学生参照下图举例:
六年级平均每班有38人,一共有6个班,六 年级一共有多少人?
教室长8 m,宽6 m,教室的面积是多少?
我们班喜欢踢球的有8人,喜欢跳绳的人数是喜欢踢球人数的1.5倍,喜欢跳绳的有多少人?
一套衣服原价400元,现在打六折出售,现价多少元?
预设
生1:求几个相同加数的和、图形的面积、一个数的几倍或几分之几是多少时,用乘法计算。
生2:求合并、移入、增加、继续往前数时,用加法计算。
生3:求剩余、比较、往回数、减少、加法逆运算时,用减法计算。
生4:求平均分配、两个量的比、乘法逆运算时,用除法计算。
⊙典型例题解析
1.课件出示例1(教材71页3题)。
为支援灾区的学生,实验小学开展了捐书活动。四年级捐120本,五年级比四年级多捐60本,六年级捐的本数是五年级的3倍。
(1)五、六年级各捐书多少本?
(2)五年级捐书的本数是四年级的几倍?
(3)六年级捐书的本数正好是二年级的5倍,二年级捐书多少本?
分析 本题综合考查学生对加、减、乘、除的意义及混合运算的掌握情况。
(1)求五年级捐书多少本,就是求比120多60的数是多少,用加法计算。
求六年级捐书多少本,就是求(120+60)的3倍是多少,用乘法计算。
(2)求五年级捐书的本数是四年级的几倍,就是求(120+60)里面有几个120,用除法计算。
(3)求二年级捐书多少本,就是把六年级捐书的本数平均分成5份,求其中的一份是多少,用除法计算。
解答 (1)120+60=180(本) 180×3=540(本)
答:五年级捐书180本,六年级捐书540本。
(2)180÷120=1.5
答:五年级捐书的本数是四年级的1.5倍。
(3)540÷5=108(本)
答:二年级捐书108本。
2.课件出示例2。
被除数、除数、余数的和是1600,已知除数是20,余数是10,则商是( )。
A.60 B.90 C.78 D.70
分析 本题考查的是对除法各部分之间关系的掌握情况。
因为被除数、除数、余数的和是1600,所以被除数=1600-20-10=1570。
又因为被除数=除数×商+余数,所以商=(被除数-余数)÷除数=(1570-10)÷20=78。
解答 C
⊙探究活动
在一个减法算式中,被减数、减数、差的和是50,已知减数是差的,这个减法算式是什么?
(1)小组合作,分析、讨论、汇报本题考查的知识点及解题思路。
预设
生1:本题考查的是对减法各部分之间关系的掌握情况。
生2:本题可以用份数来求。因为被减数=差+减数,所以当减数是差的时,减数占2份,差占3份,被减数占3+2=5(份),被减数、减数与差的和占2+3+5=10(份),求出其中的1份,就可以求出被减数、减数与差。
生3:根据求出的各部分的数值就可以写出减法算式。
生4:本题也可以用方程解答。
(2)试做,组内交流、对照计算结果后,推荐正确者板演。
预设
生1:2+3+5=10
50÷10=5
减数:2×5=10
差:3×5=15
被减数:5×5=25
算式:25-10=15
生2:设减数为2x,则差为3x,被减数为5x。
2x+3x+5x=50
x=5
2x=10 3x=15 5x=25
算式:25-10=15
(3)小结。
通过对本题的探究,大家对减法各部分之间的关系更加了解,希望大家以后可以灵活运用这些知识正确地解决相关问题。
⊙课堂总结
通过本节课的复习,你有什么收获?
⊙布置作业
教材71页1,2,4题。
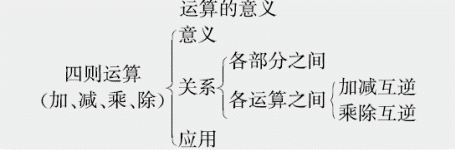
板书设计
运算的意义
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |