比
比例
各部分名称
0.9 ∶ 0.6 = 1.5
前项 后项 比值
基本性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
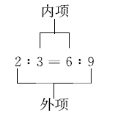
在比例里,两个内项的积等于两个外项的积。
课前准备
教师准备 多媒体课件
教学过程
⊙谈话导入
师:谁能用比的知识说一说我们班男女同学的人数情况?
(指名汇报)
师:今天我们就一起来整理和复习比和比例的有关知识。
⊙回顾与整理
1.(1)举例说一说什么是比,什么是比例,什么是比例尺以及它们的应用。
预设
生1:两个数相除又叫作两个数的比,如5÷2,可以写成5∶2。
生2:表示两个比相等的式子叫作比例,如8∶4=24∶12。
生3:图上距离和实际距离的比,叫作这幅图的比例尺,如一幅地图的比例尺是。比例尺可分为数值比例尺和线段比例尺。
生4:配制农药会应用到比的知识;地图上一般都有比例尺。
……
(2)说一说比与比例有什么区别。
| 比 | 比例 |
各部分名称 | 0.9 ∶ 0.6 = 1.5 前项 后项 比值 |
|
基本性质 | 比的前项和后项同时乘或除以相同的数(0除外),比值不变。 | 在比例里,两个内项的积等于两个外项的积。 |
(3)出示教材83页“回顾与交流”2题。
学生独立完成,思考比、分数、除法之间的关系,并全班交流。
预设
生1:除法算式中的被除数相当于分数的分子,相当于比的前项;除法算式中的除数相当于分数的分母,相当于比的后项;除号相当于分数的分数线,相当于比的比号。
生2:除法算式的商相当于分数的分数值,相当于比的比值。
强调:因为0不能作除数,所以所有分数的分母及比的后项都不能为0。
(师引导学生整理下表)
| 区别(意义) | 联系(对应部分) | |||
比(a∶b) | 表示数量间的倍比关系。 | 前项 | ∶(比号) | 后项 | 比值 |
分数() | 表示一个数。 | 分子 | —(分数线) | 分母 | 分数值 |
除法a÷b | 表示一种运算。 | 被除数 | ÷(除号) | 除数 | 商 |
(4)先想一想比的基本性质是什么,再应用比的基本性质化简下面的比。
30∶120 1∶ ∶0.1 ∶10
2.5∶6 0.5∶3.2 25∶ ∶
先思考比的基本性质,然后交流,最后独立完成,集体订正。
(5)复习按比例分配问题。
①什么是按比例分配?
(把一个数量按照一定的比进行分配,这种分配方法叫作按比例分配)
②按比例分配应用题有什么特点?
预设
生1:用比或者连比反映各部分数量占总数量的份数。
生2:直接给出各部分数量占总数量的份数。
③按比例分配应用题的一般解题步骤是什么?
预设
生:找出或求出要分配的总数量;根据已知的比求总份数;按照要分配的各部分数量占总数量的几分之几,分别求出每一部分数量是多少。
(6)完成教材83页3题。
学生独立完成,然后交流订正,并说一说解决问题时都用到了哪些知识。
2.(1)说一说。
师:我们学习了正比例和反比例的知识,请你先回忆一下,然后说一说你对这部分内容的了解。
预设
生1:我知道了什么是变化的量。
生2:我知道了什么是正比例,什么是反比例。
师:举例说明什么是变化的量。
预设
生:上学时,我走的路程的多少是随着时间的增加而增加的。路程和时间就是变化的量。
师:如果你走的速度是一定的,那么你走的路程和时间有什么关系?
生:成正比例关系。
师:你能说明理由吗?
生:我走的速度不变,走的路程随着时间的增加而增加,所以路程和时间成正比例关系。
(2)议一议。
正比例和反比例在生活中有着广泛的应用,请你想一想生活中有哪些是成正比例的量?有哪些是成反比例的量?(四人一组,互相举例说一说,并说明自己举的例子为什么是成正比例的量或者成反比例的量)
(3)全班交流。
师:每组举成正、反比例关系的实例各一个,其他小组注意不要重复,并把本组需要交流的问题展示出来。
预设
生1:买苹果时,苹果的单价一定,那么花费的总钱数和买的数量成正比例关系。如果花费的总钱数一定,苹果越便宜,买的数量就越多,苹果越贵,买的数量就越少,这时苹果的单价和数量成反比例关系。
生2:一个人走一段路程,走的速度越快,需要的时间就越短,走的速度越慢,需要的时间就越长,这时,速度和时间成反比例关系。
生3:圆的周长总是它直径的π倍,π的值是一定的,所以圆的周长和它的直径成正比例关系。
生4:给一个房间铺地砖,需要地砖的块数和地砖的面积成反比例关系,地砖的面积越大,需要的块数越少,地砖的面积越小,需要的块数越多。
……
3.课件出示:一辆汽车在高速公路上行驶,速度保持在100千米/时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
(1)提问1:这辆汽车行驶时,哪些量发生变化?哪些量不发生变化?
预设
生:汽车行驶的速度不发生变化;汽车行驶的路程随时间的增加而增加,汽车行驶的路程和行驶的时间发生变化。这时,汽车行驶的路程和行驶的时间成正比例关系。
(2)提问2:你能用哪些方式来表示这两个量之间的关系?
预设
生1:可以用列表的方式。
生2:可以用式子来表示这两个量之间的关系。
生3:也可以用画图的方式。
(3)学生活动:学生独立解决问题。
(4)学生在小组内交流,将自己的疑问记录下来。教师巡视,并对有困难的学生和小组进行个别指导。
(5)全班交流。
①提问1:表格中汽车行驶2时的路程是200千米,对应的是图中的哪个点?行驶3时的路程是多少?对应的是图中的哪个点?……(教师提问,指名汇报,集体寻找图中的对应点)
②提问2:每增加1时,路程的变化在表格中如何看出?在图中如何看出?(学生指着表格和图进行说明)
③提问3:用式子怎样把这两个量之间的关系表示出来?(指名汇报)
④提问4:每增加1时,路程的变化在式子中是如何看出的?请对应表格和图进行说明。(指名汇报)
(6)判断路程与时间是否成正比例关系,并说一说你是怎么想的。(生自由交流)
4.找出正比例和反比例的区别与联系。
通过回顾与交流,你能找出成正比例的量和成反比例的量有什么相同点和不同点吗?先在小组内交流,然后全班交流。
课件出示下表,引导学生思考正比例、反比例的区别与联系。
| 联系 | 区别 | |
变化规律 | 关系式 | ||
正比例 | 两个相关联的量,一个量变化,另一个量也随着变化。 | 两个量中的比值(商)一定。 | =k(一定) |
反比例 | 两个量的积一定。 | xy=k(一定) | |
预设
相同点:
生1:都有两个相关联的量,这两个量中一个量随着另一个量的变化而变化。
不同点:
生2:成正比例的两个量,一个量随着另一个量的增加(减少)而增加(减少);成反比例的两个量,一个量随着另一个量的增加(减少)而减少(增加)。
生3:成正比例的两个量的比值(商)是一定的,成反比例的两个量的积是一定的。
……
5.应用正、反比例知识解决问题。
提问:应用正、反比例知识解决问题的关键和步骤是什么?
(1)关键:正确判断成正比例还是成反比例是解决比例应用题的关键。
(2)步骤:
①分析数量关系,判断成什么比例。
②找等量关系。如果成正比例,按“等比”找等量关系;如果成反比例,按“等积”找等量关系。
③列比例式。设未知数为x,并带入等量关系式,得到正比例关系式或反比例关系式。
④解比例。
⑤检验并写出答语。
⊙典型例题解析
1.课件出示例1(教材84页3题)。
分析 本题考查的是学生对比例尺知识的掌握情况。
(1)先动手量出教材84页艺术小学平面图的长和宽,根据“实际距离=图上距离÷比例尺”求出实际的长和宽,再用长方形的面积计算公式求出艺术小学的实际占地面积。通过测量,图上长为14 cm,图上宽为5 cm,那么实际长为14÷=28000(cm)=280(m),实际宽为5÷=10000(cm)=100(m),实际占地面积是280×100=28000(m2)。
(2)第一问:先测量出操场的图上边长,根据“实际距离=图上距离÷比例尺”求出操场的实际边长,再用正方形的周长计算公式求操场的实际周长。通过测量,操场的图上边长为3 cm,那么实际边长为3÷=6000(cm)=60(m),绕操场跑一圈大约是60×4=240(m)。
第二问:先测量出花坛的图上半径,再求出实际半径,用圆的面积计算公式求花坛的实际占地面积。通过测量,花坛的图上半径为1 cm,那么实际半径为1÷=2000(cm)=20(m),花坛的占地面积=20×20×3.14=1256(m2)。
(3)先求出教学楼的实际占地面积,再运用“教学楼的实际占地面积÷学校的实际占地面积”或“教学楼的图上面积÷学校的图上面积”解决问题,教学楼的实际占地面积是4200 m2,4200÷28000=15%。
解答 (1)14 5 28000
(2)240 1256 (3)4200 15
2.课件出示例2。
一辆汽车从甲城开往乙城,3时行驶180千米,用这样的速度再行驶2.4时到达乙城。甲、乙两城相距多少千米?
分析 根据题意可以知道汽车行驶的速度一定,即=速度(一定)。所以汽车行驶的路程和所用的时间成正比例。汽车从甲城开往乙城用了(3+2.4)时。
解答 解:设甲、乙两城相距x千米。
=
x=324
答:甲、乙两城相距324千米。
3.课件出示例3。
硬糖每千克6.8元,软糖每千克11.6元,现要求把硬糖和软糖放在一起制成混合糖,混合糖的价格为每千克8.6元。求硬糖和软糖应取怎样的质量比才合适。
分析 对硬糖来说,混合后每千克提高了8.6-6.8=1.8(元),对软糖来说,混合后降低了11.6-8.6=3(元),而提高的总价钱应等于降低的总价钱,所以软糖的质量×3=硬糖的质量×1.8。
解答 8.6-6.8=1.8(元) 11.6-8.6=3(元)
硬糖质量∶软糖质量=3∶1.8=5∶3
答:硬糖和软糖应取5∶3的质量比才合适。
⊙探究活动
1.课件出示探究题。
甲数的等于乙数的,甲、乙两数的比是( )。
2.提出探究要求。
小组合作,探究解题思路和解题过程,看哪组解法最多。
3.交流、汇报。(小组代表发言,其他人补充)
预设
1组:根据题意,可列出下面的等式:
甲数×=乙数×
方法一 根据比例的基本性质解答。
由两个外项的积等于两个内项的积,可以得到甲数∶乙数=∶=15∶16。
方法二 用设数法解答。
设乙数为16,则甲数×=16×,甲数=12÷=15,所以甲数∶乙数=15∶16。
2组:方法一 根据乘法各部分之间的关系解答。
把乙数×看作一个整体,它是甲数×的积,则甲数=乙数×÷=乙数××=乙数×,也就是甲数是乙数的,所以甲数∶乙数=15∶16。
方法二 根据倒数知识解答。
假设等号左右两边的结果都为1,则甲数×=1,甲数=,乙数×=1,乙数=,所以甲数∶乙数=∶=15∶16。
4.小结。
解答此类题可以灵活运用比例的基本性质、设数法等。
⊙课堂总结
通过本节课的学习,你有什么收获?
⊙布置作业
教材84页1、4、5题。
板书设计
正比例与反比例
比:两个数相除又叫作两个数的比。
比例:表示两个比相等的式子叫作比例。
比例尺:图上距离和实际距离的比,叫作这幅图的比例尺。比例尺可分为数值比例尺和线段比例尺。
正比例、反比例:
相同点:都有两个相关联的量,这两个量中一个量随着另一个量的变化而变化。
不同点:
(1)成正比例的两个量,一个量随着另一个量的增加(减少)而增加(减少);成反比例的两个量,一个量随着另一个量的增加(减少)而减少(增加)。
(2)成正比例的两个量的比值(商)是一定的,成反比例的两个量的积是一定的。
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |