设计说明
1.重视对旧知的复习,为学习新知做好准备。
在复习导入的过程中,教师出示了大量相关联的量,让学生判断这些相关联的量是否成正比例。这样不仅能使学生感受到生活中存在着大量成正比例关系的量,还能使学生进一步巩固判断两个量是否成正比例的方法。
2.突出自主探究的学习过程。
在新知探究环节,遵循以学生为主体的原则,通过让学生在方格纸上描出并连接成正比例的量所对应的点,认识并掌握正比例图象的特点。
3.及时反馈,巩固学习成果。
在反馈应用环节,引导学生以自主探究和合作交流的方式理解正比例图象,并应用正比例图象解决问题。让学生在自主讨论中利用图象,不计算,由一个量的值直接找到对应的另一个量的值,从而巩固所学知识,提高应用能力。
课前准备
教师准备 多媒体课件
学生准备 方格纸
教学过程
⊙复习导入
1.复习旧知。
课件出示:
(1)什么样的两个量叫作成正比例的量?
(2)判断下面的量是否成正比例。
①每行人数一定,总人数与行数。
②长方体的底面积一定,体积与高。
③长方形的周长一定,长与宽。
④圆的周长与半径。
2.导入新课,明确学习目标。
我们已经知道了正比例的意义,并且学会了判断两个相关联的量是否成正比例,那么我们能否用图象的形式去直观表示两个成正比例的量的变化关系呢?这节课,我们就一起来探究这个问题。
设计意图:先通过复习进一步理解正比例的意义及巩固判断两个量是否成正比例的方法,再直接揭示学习内容,使学生明确本节课的学习任务。
⊙探究新知
1.认识正比例图象。
(1)课件出示教材44页表格。
全班同学去看电影,看电影的人数与所付票费如下表。
人数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
票费/元 | 0 | 2 | 4 | 6 |
|
|
|
|
| … |
组织学生把上表填写完整,并判断看电影的人数与所付票费是否成正比例。
(学生口头回答,教师课件完成)
(2)观察、交流。
①从上表中,你发现了什么?想到了什么?
预设
生1:我发现看电影的人数和所付票费是两个相关联的量,人数扩大到原来的2倍,票费也扩大到原来的2倍,票费随人数的变化而变化。
生2:我发现看电影的人数和所付票费的比值是一定的。
生3:我想到了这两个量成正比例关系。
生4:我想到了是否可以用图象来表示这两个量的关系。
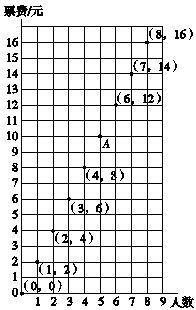
②课件出示教材44页下面的图。
师:根据表格说出下图中各点的含义。

[引导学生结合数对知识,说出图中各点的含义,如点(4,8)表示人数是4时,所需票费是8元]
(3)操作、汇报。
连接图上各点,你发现了什么?
(所描的点在同一条直线上)
(4)明确正比例图象的特点。
当两个变量成正比例关系时,所绘成的图象是一条直线。
2.点A是直线上一点,这一点表示什么含义?小明说点(100,200)也在这条直线上,你认为他说得对吗?
(小组内交流后汇报)
设计意图:让学生先填表判断全班同学去看电影,看电影的人数与所付票费是否成正比例,再将这组数据用“描点法”画在方格纸上,用图的形式去直观表示两个成正比例的量的变化关系。促使学生在合作探究中认识并掌握正比例图象的特点,提高学生学习数学及应用数学的能力。
⊙反馈应用
1.课件出示教材45页“练一练”1题。
(1)乘船的人数与所付船费如下表。
人数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
船费/元 | 0 | 5 | 10 | 15 |
|
|
|
| … |
说一说你从表中获得的信息,并把上表填写完整。
(指名汇报)
(2)把表中的数据用下图表示。
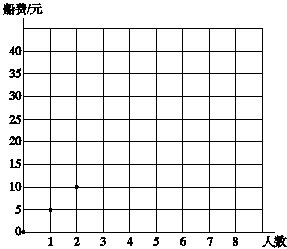
(3)先根据上表描点,再顺次连接各点,你发现了什么?(这些点都在同一条直线上)
(4)点(8,40)在这条直线上吗?这一点表示什么含义?
(5)根据图象判断,5个人乘船所需的船费是多少钱?付船费35元,乘船的人数是多少?
(5个人乘船所需的船费是25元;付船费35元,乘船的人数是7人)
2.出示课堂活动卡。
⊙课堂总结
通过这节课的学习,你获得了哪些知识?
⊙布置作业
教材45页“练一练”2题。
板书设计
画一画
方法:填表格→描点→连线
作用:直线→找点→求值
正比例的图象是一条直线。
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |