设计说明
1.创设问题情境,激发学习兴趣。
兴趣是最好的老师。新课伊始,为学生创设“圆柱形橡皮泥的体积你会求吗?”的问题情境,引导学生经过思考、讨论、交流,找到解决的方法。这样的设计不仅自然渗透了圆柱(新问题)和长方体(已知)的知识联系,还让学生体会到可以有许多方法去解决生活中的实际问题,激发了学生的学习兴趣和探究新知的欲望。
2.实践操作,促进知识迁移。
知识和经验的积累来源于大量的实践活动。动手操作不但能使学生获得感性的体验,更能加深学生对知识的理解。本设计为学生创设动手操作的情境,使学生通过动手拼摆,充分感知图形之间的关系,深刻理解圆柱的体积公式的合理性,充分认识到图形转化过程中形变而质不变的辩证关系,使学生在把旧知迁移、发展、转化、构建为新知的同时,动手操作、观察及归纳能力也得到极大的提高。
课前准备
教师准备 圆柱的体积公式演示教具 多媒体课件
学生准备 圆柱的体积公式演示学具
教学过程
第1课时 圆柱的体积(1)
⊙创设情境,导入新课
1.出示一块圆柱形橡皮泥。
师:同学们,我们以前学过长方体和正方体体积的计算方法,现在我想知道这块圆柱形橡皮泥的体积是多少,你有好的办法吗?
2.学生小组讨论交流并汇报。
预设
生1:可以把这块橡皮泥捏成长方体,利用长方体的体积公式来解决。
生2:可以把它放到量杯中,计算上升的水的体积。
3.引入新课。
解决生活中的问题有很多方法,需要我们去发现、去探究。这节课我们就共同去探究圆柱体积的计算方法。
设计意图:通过创设问题情境,引发学生思考,进一步体会“转化”思想。
⊙新知探究
1.利用知识的迁移,猜想圆柱体积的计算方法。
(1)提出猜想。
师:在刚才的问题中同学们提出可以将圆柱形橡皮泥捏成长方体,这时会有什么变化?
(形状变了,体积没变)
师:我们已经掌握了长方体、正方体的体积计算方法,大家猜一猜:圆柱体积可能等于底面积×高吗?
(2)学生讨论、交流。
2.探究算法。
(1)提出问题:能不能借鉴把圆转化为长方形的方法,把手中的圆柱形学具转化为长方体?
(2)动手操作:把圆柱转化为长方体。
(3)汇报交流:介绍自己的转化方法。
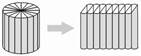
(结合学生回答,课件演示转化过程:先沿圆柱底面的半径把圆柱平均分成16份,然后拼成一个近似的长方体)

(4)引导学生明确:由于我们分得不够细,所以看起来还不太像长方体;分得越多,拼成的立体图形就越接近长方体。(课件演示将圆柱分成更多等份并拼成一个近似的长方体的过程)
(5)汇报发现。
①拼成的长方体的体积与圆柱的体积有什么关系?
②长方体的底面积、高分别与圆柱的底面积、高有什么关系?
③长方体的体积等于什么?圆柱呢?
3.总结公式。
(1)圆柱的体积怎样计算?为什么?
(圆柱通过分割、拼组,可以转化成近似的长方体。这个近似的长方体的底面积与圆柱的底面积相等,高与圆柱的高相等。因为长方体的体积等于底面积乘高,所以圆柱的体积=底面积×高)
(2)说一说,怎样用字母表示圆柱的体积公式?
(学生反馈:V=Sh)
(3)如果已知d、r、C和h,怎样求圆柱的体积?
求圆柱体积的直接条件是S、h,间接条件是d、r和C,所以圆柱的体积公式也可以表示为V=πr2h、V=πh、V=πh。
(4)圆柱和长方体、正方体一样,都是直柱体,你能总结出求它们的体积的统一计算方法吗?
(直柱体的体积都等于底面积×高)
⊙巩固提升
1.完成教材9页“练一练”1题。
(使学生明白长方体、正方体、圆柱的体积都可以用底面积×高求出)
2.完成教材9页“练一练”2题。
(注意培养学生的识图能力和灵活应用公式的能力)
3.完成教材9页“练一练”3题。
(先分析题意,找到解决问题的关键:求出圆柱形杯子的容积,再比较,最后解决问题)
设计意图:通过设计不同层次的习题,既巩固了对新知识的理解,又培养了学生利用新知识解决问题的能力。
⊙课堂总结
通过这节课的学习,你收获了什么?圆柱的体积怎样计算?
⊙布置作业
教材10页“练一练”6题。
板书设计
圆柱的体积(1)
长方体的体积=底面积×高
↓ ↓ ↓
圆柱的体积=底面积×高
V =S × h
V = πr2 × h
第2课时 圆柱的体积(2)
⊙复习引入
1.填空。
把圆柱的底面分成许多相等的扇形,然后把圆柱切开,就能拼成一个近似的长方体。这个长方体的底面积等于圆柱的( ),高等于圆柱的( ),长方体的体积等于( ),因此,圆柱的体积等于( )。
2.算一算。
学校为了用水方便,计划在校园里建一个圆柱形蓄水池。圆柱形蓄水池的底面直径是4米,高是3米。
(1)这个圆柱形蓄水池的占地面积是多少?
师:求这个圆柱形蓄水池的占地面积也就是求什么?(求圆柱的底面积)求圆柱的底面积用到哪个公式?
(2)要建这个圆柱形蓄水池,需要挖土多少立方米?
师:这个问题求的又是什么呢?(求圆柱的体积)圆柱的体积计算公式是什么?
(3)学生独立总结,并算一算。
3.引入新课。
师:这节课,我们学习圆柱的体积计算公式的应用。
设计意图:“温故”是“知新”的基础。通过复习,让学生进一步掌握圆柱体积的计算方法,为下一步应用圆柱体积的计算方法解决实际问题作铺垫,让学生体会到新知识与旧知识之间的联系,充分体现数学知识的前后连贯性。
⊙建构模型,探究新知
1.课件出示教材9页“试一试”。
金箍棒底面周长是12.56 cm,长是200 cm。这根金箍棒的体积是多少立方厘米?
(1)学生独立思考:要求这根金箍棒的体积先求什么?再求什么?
(2)小组内交流自己的想法。(引导学生明确在不知道底面积的情况下,可先根据底面周长求出底面半径,再利用体积公式进行计算)
(3)汇报交流。
3.14×(12.56÷3.14÷2)2×200
=3.14×4×200
=2512(cm3)
答:这根金箍棒的体积是2512 cm3。
2.如果这根金箍棒是铁制的,每立方厘米铁的质量为7.9 g,这根金箍棒的质量为多少千克?
(1)学生独立思考。
(2)汇报交流。
2512×7.9=19844.8(g)=19.8448(kg)
答:这根金箍棒的质量为19.8448 kg。
设计意图:引导学生通过自主探究、合作交流的方式寻求解决问题的方法,促使学生能灵活地运用已学的数学知识解决一些简单的数学问题,培养学生分析问题、解决问题的能力,加深对圆柱体积知识的理解和巩固。
⊙联系实际,解决问题
1.一个装满稻谷的圆柱形粮囤,底面积为2 m2,高为80 cm。每立方米稻谷约重600千克,这个粮囤存放的稻谷约重多少千克?
(1)通过读题,你发现了什么?(要换算单位)
(2)要求这个粮囤能存放多少稻谷,必须先求什么?(先求体积)
(3)明确题意后,独立计算。
2.一个圆柱,侧面展开后是一个边长为9.42 dm的正方形。这个圆柱的体积是多少立方分米?
设计意图:让学生根据圆柱的体积计算方法解决不同的实际问题,培养学生灵活解决实际问题的能力,让学生充分感受到数学与现实生活的联系。
⊙综合运用,拓展延伸
1.完成教材10页“练一练”7题。
(引导学生通过计算,体会测量不规则物体体积的方法,提高学生解决实际问题的能力)
2.实践活动:设计一个方案,测量并计算出1枚1元硬币的体积。
⊙课堂总结
通过这节课的学习,你有什么收获?
⊙布置作业
教材10页“练一练”9题。
板书设计
圆柱的体积(2)
3.14×(12.56÷3.14÷2)2×200
=3.14×4×200
=2512(cm3)
2512×7.9=19844.8(g)=19.8448(kg)
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |