教案设计
设计说明
本节课本着“让学生的自主探究活动贯穿课堂的始终”的原则,让学生充分自主学习,通过研究、讨论、操作,从而得出结论,激发了学生的学习兴趣,培养了学生的思维能力和实践操作能力。
1.为学生自主学习创造条件。
在教学设计中,发展学生的自主学习能力。一个问题的解决是学生认识上的一个跨越,只有留给学生充分的时间,学生才能有所发现、有所创造。所以在把长方体的展开图展现在学生面前时,要留给学生充分的思考时间,这样才能促进学生的思维发展,让学生的思维在思考的过程中不断得到完善。
2.以动手操作促进学生的思维发展。
在教学长方体的表面积的计算方法时,先让学生动手展开长方体,展示出6个面。通过对比长方体与其展开图,深刻地体会长方体各个面的面积之和就是它的表面积,掌握长方体6个面之间的关系,抓住推导长方体的表面积的计算方法的关键,然后让学生通过小组合作共同探究长方体的表面积的计算方法。在这一过程中,让学生充分发表自己的见解,选择适合自己的方法,不但调动了学生学习的积极性,更有助于学生形成探究性的学习习惯,培养创新意识。
课前准备
教师准备 PPT课件、长方体纸盒
学生准备 长方体纸盒、剪刀
教学过程
⊙创设情境,激趣引入
1.创设情境,提出问题。
手工课上,同学们要做一个长方体包装盒,老师提出了制作要求:长是7厘米,宽是5厘米,高是3厘米。做一个这样的长方体包装盒至少要用多少纸板呢?(学生交流)
2.这就是我们这节课要学习的新知识——长方体的表面积。
设计意图:在新课的开始,创造一个动手操作的活动,既能激发学生的学习兴趣,又能引出新知,为新课的学习作铺垫。
⊙启发引导,探究新知
1.建立长方体与其展开图之间的对应关系。
(1)课件出示长方体纸盒(6个面都是长方形),提出探究问题。
①把这个长方体纸盒展开后,在展开图上你能找到长方体纸盒的各个面吗?
②你能根据长方体的长、宽、高确定展开后每个长方形的长和宽吗?
(2)组织学生四人一组,展开长方体纸盒并做好标注。
(3)学生展示长方体纸盒的展开图,说明每个长方形与原长方体长、宽、高的关系。
方法一 全部拆开,把相对的面摆放在一起组成三大部分。

方法二 把长方体纸盒剪成面积相等的两大部分。

方法三 把长方体纸盒的6个面剪成上、下面和4周三部分。
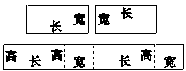
设计意图:让学生经历把长方体展开的过程,进一步了解立体图形与平面图形的关系,培养空间观念,为下面探究表面积的计算方法作铺垫。
2.探究长方体的表面积的计算方法。
(1)课件出示例题:做一个这样的包装盒至少要用多少纸板?(单位:cm)
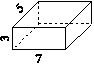
(2)理解概念。
①思考:求至少要用多少纸板就是求什么。(所有面的面积之和)
②呈现概念:长方体6个面的面积之和叫作它的表面积。
(3)探究算法。
①思路点拨:求至少要用多少纸板就是求这个长方体6个面的面积总和是多少,也就是求它的表面积。
②学生独立思考,尝试计算。
③算法展示。
算法一 先分别计算出6个面的面积,然后算总和。
7×5+5×3+7×3+7×5+5×3+7×3=142(cm2)
算法二 先分别算出上、下,前、后,左、右面的面积和,然后算总和。
7×5×2+5×3×2+7×3×2
=70+30+42
=142(cm2)
算法三 先算出上、前、左这三个面的面积和,然后再乘2。
(7×5+5×3+7×3)×2
=71×2
=142(cm2)
④优化算法,比较哪种算法最简单。(算法三最简单)比较算法二与算法三有什么不同。它们之间有什么联系?(都是只计算出3个面的面积,再乘2。这两个算式可以应用乘法分配律互相转化)
(4)总结长方体的表面积的计算公式。
师:通过上面的计算,你能总结出长方体的表面积的计算公式吗?
(根据学生的回答,板书长方体的表面积的计算公式)
长方体的表面积=(长×高)×2+(宽×高)×2+(长×宽)×2
长方体的表面积=(长×高+宽×高+长×宽)×2
(5)尝试练习。
做一个长方体木箱,要使这个木箱的长、宽、高分别是5分米、4分米、3分米,那么做这样一个木箱至少需要用木板多少平方分米?
设计意图:让学生经历计算、比较、自主探究、合作交流、尝试练习等多种学习方式计算长方体的表面积,在展示算法的过程中,借鉴他人在计算上的简便之处,从而总结出长方体的表面积的计算方法。
3.探究正方体的表面积的计算方法。
(1)课件演示:把上面长方体的长、宽、高都变成5厘米。
学生借鉴长方体的表面积的计算方法,尝试总结正方体的表面积的计算方法。
师:这个长方体变成了什么形状?(正方体)你能用比较简单的方法计算出它的表面积吗?
学生讨论后得出:
①正方体的各个面都是相等的正方形,只要计算出一个面的面积,再乘6就可以求出正方体的表面积。
②正方体展开后,每个正方形的边长都与棱长相等。
(2)如何计算正方体的表面积?
[5×5×6=150(cm2)]
(3)小结:正方体的表面积=棱长×棱长×6。
(4)尝试练习。
给棱长为40分米的正方体木箱的表面涂上油漆,涂油漆部分的面积是多少平方分米?
设计意图:根据正方体是特殊的长方体,运用类比的方法,让学生自己从长方体的表面积的计算方法中推导出正方体的表面积的计算方法。这样不仅提高了学生的逻辑思维能力,而且培养了学生的再创造能力。
⊙巩固应用,及时反馈
1.计算下面各立体图形的表面积。
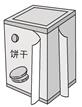
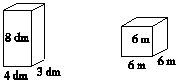
2.给棱长为0.8米的正方体木箱的表面涂上油漆(下底面不涂),涂油漆部分的面积是多少?
3.饼干盒长20厘米,宽15厘米,高30厘米,要在它的四周贴上商标纸,这张商标纸的面积至少是多少平方厘米?
设计意图:通过多种形式的练习,使学生熟练掌握长方体和正方体的表面积的计算公式,并能应用所学知识解决实际问题,提高学生分析问题和解决问题的能力。
⊙课堂总结
通过今天的学习你们有什么收获?你们感受最深的是什么?
⊙布置作业
教材17页1、2、3、4题。
板书设计
长方体的表面积
长方体(或正方体)6个面的总面积叫作它的表面积。
长方体的表面积=长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |