1．课件出示典型例题1。课前准备
教师准备 PPT课件
教学过程
⊙谈话揭题
之前，我们复习了平面图形的周长、表面积以及立体图形的表面积、体积等知识。这节课，我们就在综合运用平面图形和立体图形的知识解决问题的过程中充分体会平面图形与立体图形之间的区别和联系。(板书课题：平面图形与立体图形的综合应用)
⊙回顾与整理
1．思考：在解答平面图形的周长和表面积的问题时，要注意什么？
教师结合学生的回答明确：在解答平面图形的周长和表面积的问题时，要注意发现比较隐蔽的条件，还要想办法把复杂的问题转化为比较简单的求平面图形的周长和面积的问题。
2．思考：在解答立体图形的表面积的问题时，要注意什么？
(1)学生小组讨论、汇报。
(2)教师小结。
①把一个立体图形分成两部分，新增加的表面积等于切面面积的2倍。
②把两个立体图形黏合到一起，减少的表面积等于黏合面积的2倍。
③若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来；若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。
3．思考：在解答立体图形的体积的问题时，要注意什么？
(1)学生分组进行讨论，教师适当引导。
(2)学生汇报。
(3)教师小结。
①把一种形状的物体变成另一种形状的物体后，形状变了，但它的体积不变。
②物体全部浸没在水中(水未溢出)，上升部分的水的体积等于物体的体积；把全部浸没在水中的物体取出，下降部分的水的体积等于物体的体积。
③以一个长方形的长(宽)为轴旋转，得到的立体图形为圆柱，圆柱的高是长方形的长(宽)，底面半径是长方形的宽(长)；如果以一个正方形的边长为轴旋转，则得到的圆柱的高与底面半径都等于正方形的边长。
……
⊙典型例题解析
1．课件出示典型例题1。
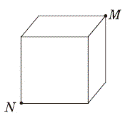
如图，在正方体的顶点M处有一只蜗牛，在N处有一片树叶，现在蜗牛想吃树叶，请你画出蜗牛爬行的最短路线。
分析 本题考查的是学生的空间想象能力及对展开图与立体图形的关系的了解。
“在平面内，两点间的线段最短”，把已知的立体图形展开后连线。展开后发现点M、N分别是由2个小正方形所组成的一个大长方形的一组相对的顶点(如右图)。
解答 取正方体的棱长AB的中点O(如下图)，连接ON、OM即可。
2．课件出示典型例题2。
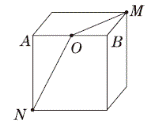
一个直角三角形(如下图)，分别沿着其中的一条直角边旋转一周都能得到一个圆锥，怎样旋转得到的圆锥的体积较大？
分析 以直角三角形的一条直角边为轴旋转一周可以得到一个圆锥。不动的直角边是圆锥的高，另一条直角边是圆锥的底面半径。
解答 以BC边为轴：×3.14×302×40＝37680(cm3)
以AB边为轴：×3.14×402×30＝50240(cm3)
因为50240＞37680，所以以AB边为轴旋转得到的圆锥的体积较大。⊙探究活动
1．出示探究题目。
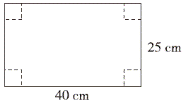
有一块长40 cm、宽25 cm的长方形铁皮(如右图)，在四个角上分别剪去面积相等的正方形后，正好可以折成一个深5 cm的无盖长方体铁盒，求这个铁盒的体积。
2．小组合作，探究解法。
3．教师讲解解题思路。
在长方形铁皮的四个角上分别剪去面积相等的正方形后，所折成的无盖长方体铁盒的深度正好是四个小正方形的边长。因此该铁盒的长是(40－2×5)cm，宽是(25－2×5)cm，高是5 cm。根据“长方体的体积＝长×宽×高”可求出铁盒的体积。
4．学生解答。
(40－2×5)×(25－2×5)×5
＝30×15×5
＝2250(cm3)
答：这个铁盒的体积是2250 cm3。
⊙全课总结
通过本节课的复习，你有什么收获？
⊙布置作业
1．教材90页11题。
2．教材91页12题。
板书设计
平面图形与立体图形的综合应用
结合图形，展开想象，
具体问题，具体分析。
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |