知识点一 日历中的集合问题3 时间与数学
备课解决方案
备教材内容
1．本课时学习的是教材78～79页的内容。
2．年、月、日的知识在生活中经常用到，具有常识性，而且其中蕴涵着丰富的数学信息，包含着许多规律，与数学有着密不可分的联系。
3．本节课教学的内容就是探究并解决与日历有关的实际问题，引导学生从中发现各种规律，进一步提高学生观察、发现和独立思考的能力。从日历中寻找有关的信息，在解决问题的过程中学会运用做记号、一一列举的策略，在具体操作的过程中感受时间与数学的密切联系，初步学会用数学思维方式去分析、解决日常生活中的一些基本问题，感受集合的思想。
备已学知识
年、月、日：一年有12个月，平年有365天，闰年有366天。
9月是小月，共有30天，一个星期有7天。
备教学目标
知识与技能
1．结合共同的休息日这一常见的生活现象，探究与时间有关的现实问题。
2．引导学生借助日历，运用做记号、一一列举等策略找出奇思一家共同的休息日，正确填写集合图。探究并掌握解决这类问题的基本方法。
过程与方法
1．在观察比较、发现规律的现实活动中，进一步提高观察和发现的能力。
2．了解日历中蕴涵的丰富的数学信息，初步感受数学集合思想。
情感、态度与价值观
1．在解决实际问题的过程中，了解日历中蕴涵的丰富的数学信息。
2．培养学生发现问题、解决问题的能力和合作意识，使学生进一步感受数学与日常生活的密切联系，树立学好数学的信心。
备重点难点
重点：通过对奇思一家共同的休息日这一具体问题的探究，掌握解决这类问题的基本方法。
难点：初步感受集合思想。
备知识讲解
知识点一 日历中的集合问题
问题(1)导入 奇思的父亲是火车司机，每工作3天后休息1天。奇思的母亲是飞机乘务员，每工作1天后休息1天。奇思是周六、周日休息。(教材78页例题)
9月份
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|
|
|
| 1 | 2 | 3 |
4 | 5 | 6 | 7 | 8 | 9 | 10 |
11 | 12 | 13 | 14 | 15 | 16 | 17 |
18 | 19 | 20 | 21 | 22 | 23 | 24 |
25 | 26 | 27 | 28 | 29 | 30 |
|
(1)用△标出父亲的休息日，用○标出母亲的休息日。你发现了什么？
(2)再用√标出奇思的休息日。你又发现了什么？
过程讲解
1．理解题意
(1)奇思的父亲每工作3天后休息1天，所以从9月1日开始，依次标出4号、8号、12号……4的倍数号休息。
(2)奇思的母亲每工作1天后休息1天，所以从9月1日开始，依次标出2号、4号、6号……2的倍数号休息。
(3)奇思是周六、周日休息，把9月份中全部的周六、周日标出来。
2．解决问题——找出父亲、母亲及奇思的休息日
奇思的父亲、母亲及奇思的休息日标出情况如下：
9月份
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|
|
|
| 1 | 2○ | 3√ |
4△○√ | 5 | 6○ | 7 | 8△○ | 9 | 10○√ |
11√ | 12△○ | 13 | 14○ | 15 | 16△○ | 17√ |
18○√ | 19 | 20△○ | 21 | 22○ | 23 | 24△○√ |
25√ | 26○ | 27 | 28△○ | 29 | 30○ |
|
发现：
(1)父亲的休息日都是4的倍数，母亲的休息日都是2的倍数，奇思的休息日没有特殊的规律。
(2)同时标有△和○的日子有4号、8号、12号、16号、20号、24号和28号，这些日子都是奇思的父母同时在家的日子。
(3)同时标有△、○和√的日子只有4号和24号，这些日子奇思和父母同时在家。
问题(2)导入 第一幅图表示的是父母共同的休息日，你看懂了吗？请你也像这样表示出其他的休息日。(教材78页例题)
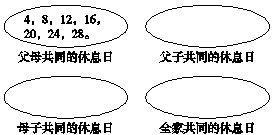
过程讲解
1．理解题意
根据问题(1)中的答案，从表中找出同时标有相应标记的日期，并填写集合。
思想方法 解读 用集合圈表示奇思一家三口的休息日，渗透了集合思想。集合思想就是运用集合的概念、逻辑语言、运算、图形等来解决数学问题或非数学问题的一种思想。 |
第一个是父母共同的休息日集合，也就是表中同时标有△和○的日期。
第二个是父子共同的休息日集合，也就是表中同时标有△和√的日期。
第三个是母子共同的休息日集合，也就是表中同时标有○和√的日期。
第四个是全家共同的休息日集合，也就是表中同时标有△、○和√的日期。
2．解决问题
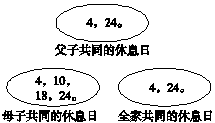
归纳总结
解决此类问题要先依据题目的要求找到各自单独的信息，做好标记，再归类到各自的集合圈内，然后找到重复出现的部分。
知识点二 日历中的规律
问题导入 观察日历，找规律。(教材79页例题)
9月份
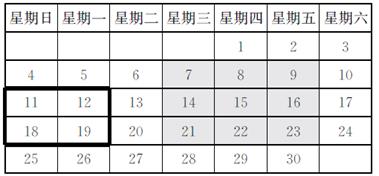
(1)观察日历中加框的4个数，你发现了什么？
(2)观察日历中有阴影的9个数，你又发现了什么？
(3)你还能在日历中找到什么规律？
过程讲解
1．解决问题(1)
观察加框的4个数，表中加框的4个数分别是11，12，18，19。这4个数左右、上下相邻，左右相差1，上下相差7。此外，对角上的两个数相加的和相等。
(1)横向看左右两列，右边的数都比左边的数大1。
(2)纵向看上下两行，下面的数都比上面的数大7。
(3)对角上的2个数相加的和分别是11＋19＝30，12＋18＝30，和相等。
2．解决问题(2)
可以从行、列、对角等不同的角度入手，观察各行、各列、两个对角上的数的大小、排列规律以及它们的差、和的变化规律。
(1)每行中的3个数从左到右依次增加1。
(2)每列中的3个数从上到下依次增加7。
(3)三行中各行3个数的和分别是7＋8＋9＝24，14＋15＋16＝45，21＋22＋23＝66，都等于各行中间数的3倍，并且各行3个数的和从上到下依次增加21；三行中9个数的和是中间数15的9倍，即15×9＝135。
(4)以中间数15为中心，横着看，14＋15＋16＝45；竖着看，8＋15＋22＝45；对角上的3个数相加的和分别是7＋15＋23＝45，9＋15＋21＝45，都等于中间数15的3倍。
3．解决问题(3)
可以再扩大一下范围或从总体上观察每行、每列的数，有如下规律：
(1)每行中的数从左到右依次增加1。
(2)每列中的数从上到下依次增加7。
……
归纳总结
日历中的数有很多规律，如横向左边的数比右边的数少1；纵向上面的数比下面的数少7等。
备易错易混
误区 小明每周学习篮球的时间是周一和周四，小东每周学习篮球的时间是周四和周五，小强每周学习篮球的时间是周一和周四。
因此可以得出：小明、小东和小强共同学习篮球的时间是周一、周四和周五。
错解分析 此题错在把每个人学习篮球的时间误以为是三个人共同学习篮球的时间了。
错解改正 小明、小东和小强共同学习篮球的时间是周四。
温馨提示
可以利用集合的方法找到三个人共同学习篮球的时间。
备综合能力
能力点一 运用移多补少法解决日历中的规律问题
例1 下面每个方框中三个日期的排列有什么规律？根据你发现的规律判断小明所圈的日期可能是多少。
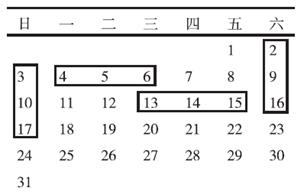
分析 横向方框中的三个日期从左到右依次多1，纵向方框中的三个日期从上到下依次多7。每个方框中三个日期的和都是中间那个日期的3倍。
小明圈的三个日期的和是21，21÷3＝7，说明中间的那个日期是7，其余两个日期有可能是0和14或6和8，日历上没有0，所以小明圈的日期是6，7，8。
解答 横向方框中的三个日期从左到右依次多1，纵向方框中的三个日期从上到下依次多7。每个方框中三个日期的和都是中间那个日期的3倍。
21÷3＝7 7－1＝6 7＋1＝8
小明圈的日期是6，7，8。
2．解决问题——找出父亲、母亲及奇思的休息日
奇思的父亲、母亲及奇思的休息日标出情况如下：
9月份
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|
|
|
| 1 | 2○ | 3√ |
4△○√ | 5 | 6○ | 7 | 8△○ | 9 | 10○√ |
11√ | 12△○ | 13 | 14○ | 15 | 16△○ | 17√ |
18○√ | 19 | 20△○ | 21 | 22○ | 23 | 24△○√ |
25√ | 26○ | 27 | 28△○ | 29 | 30○ |
|
发现：
(1)父亲的休息日都是4的倍数，母亲的休息日都是2的倍数，奇思的休息日没有特殊的规律。
(2)同时标有△和○的日子有4号、8号、12号、16号、20号、24号和28号，这些日子都是奇思的父母同时在家的日子。
(3)同时标有△、○和√的日子只有4号和24号，这些日子奇思和父母同时在家。
问题(2)导入 第一幅图表示的是父母共同的休息日，你看懂了吗？请你也像这样表示出其他的休息日。(教材78页例题)
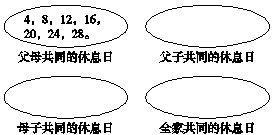
过程讲解
1．理解题意
根据问题(1)中的答案，从表中找出同时标有相应标记的日期，并填写集合。
思想方法 解读 用集合圈表示奇思一家三口的休息日，渗透了集合思想。集合思想就是运用集合的概念、逻辑语言、运算、图形等来解决数学问题或非数学问题的一种思想。 |
第一个是父母共同的休息日集合，也就是表中同时标有△和○的日期。
第二个是父子共同的休息日集合，也就是表中同时标有△和√的日期。
第三个是母子共同的休息日集合，也就是表中同时标有○和√的日期。
第四个是全家共同的休息日集合，也就是表中同时标有△、○和√的日期。
2．解决问题
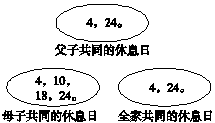
归纳总结
解决此类问题要先依据题目的要求找到各自单独的信息，做好标记，再归类到各自的集合圈内，然后找到重复出现的部分。
知识点二 日历中的规律
问题导入 观察日历，找规律。(教材79页例题)
9月份
(1)观察日历中加框的4个数，你发现了什么？
(2)观察日历中有阴影的9个数，你又发现了什么？
(3)你还能在日历中找到什么规律？
过程讲解
1．解决问题(1)
观察加框的4个数，表中加框的4个数分别是11，12，18，19。这4个数左右、上下相邻，左右相差1，上下相差7。此外，对角上的两个数相加的和相等。
(1)横向看左右两列，右边的数都比左边的数大1。
(2)纵向看上下两行，下面的数都比上面的数大7。
(3)对角上的2个数相加的和分别是11＋19＝30，12＋18＝30，和相等。
2．解决问题(2)
可以从行、列、对角等不同的角度入手，观察各行、各列、两个对角上的数的大小、排列规律以及它们的差、和的变化规律。
(1)每行中的3个数从左到右依次增加1。
(2)每列中的3个数从上到下依次增加7。
(3)三行中各行3个数的和分别是7＋8＋9＝24，14＋15＋16＝45，21＋22＋23＝66，都等于各行中间数的3倍，并且各行3个数的和从上到下依次增加21；三行中9个数的和是中间数15的9倍，即15×9＝135。
(4)以中间数15为中心，横着看，14＋15＋16＝45；竖着看，8＋15＋22＝45；对角上的3个数相加的和分别是7＋15＋23＝45，9＋15＋21＝45，都等于中间数15的3倍。
3．解决问题(3)
可以再扩大一下范围或从总体上观察每行、每列的数，有如下规律：
(1)每行中的数从左到右依次增加1。
(2)每列中的数从上到下依次增加7。
……
归纳总结
日历中的数有很多规律，如横向左边的数比右边的数少1；纵向上面的数比下面的数少7等。
备易错易混
误区 小明每周学习篮球的时间是周一和周四，小东每周学习篮球的时间是周四和周五，小强每周学习篮球的时间是周一和周四。
因此可以得出：小明、小东和小强共同学习篮球的时间是周一、周四和周五。
错解分析 此题错在把每个人学习篮球的时间误以为是三个人共同学习篮球的时间了。
错解改正 小明、小东和小强共同学习篮球的时间是周四。
温馨提示
可以利用集合的方法找到三个人共同学习篮球的时间。
备综合能力
能力点一 运用移多补少法解决日历中的规律问题
例1 下面每个方框中三个日期的排列有什么规律？根据你发现的规律判断小明所圈的日期可能是多少。
分析 横向方框中的三个日期从左到右依次多1，纵向方框中的三个日期从上到下依次多7。每个方框中三个日期的和都是中间那个日期的3倍。
小明圈的三个日期的和是21，21÷3＝7，说明中间的那个日期是7，其余两个日期有可能是0和14或6和8，日历上没有0，所以小明圈的日期是6，7，8。
解答 横向方框中的三个日期从左到右依次多1，纵向方框中的三个日期从上到下依次多7。每个方框中三个日期的和都是中间那个日期的3倍。
21÷3＝7 7－1＝6 7＋1＝8
小明圈的日期是6，7，8。
总结
发现日历中的排列规律是解决此类问题的关键。
能力点二 运用假设法解决有关出生月份的问题
例2 实验小学三(1)班数学小组有14名同学，这14名同学至少有几名同学的生日在同一个月？
分析 1年有12个月，假设每一个月都有同学过生日，12个月就有12名同学过生日，如下图所示：
一共有14名同学，还有2名同学也在这12个月中的某一个月过生日。假设这2名同学的生日不在同一个月，这14名同学也一定有2名同学的生日在同一个月。
解答 这14名同学至少有2名同学的生日在同一个月。
提示
解决此题可以运用假设法，要考虑全面，例如上题中也许这14名同学都在同一个月过生日，最不凑巧的情况下只有2名同学在同一个月过生日。
备教学资料
少年高斯的故事
科学家高斯出生在一个贫穷的家庭。高斯在三岁时，一天晚上他看见父亲在算工钱，还帮忙纠正父亲计算的错误。长大后他成为了杰出的天文学家、数学家。他在物理的电磁学方面也有一些贡献，现在电磁学的一个单位就是用他的名字命名的。数学家们则称呼他为“数学王子”。
高斯八岁时进入乡村小学读书。教数学的老师是从城里来的，他觉得在穷乡僻壤的地方教书是大材小用。而他又有些偏见，认为穷人的孩子天生就是笨蛋，教这些孩子念书不必认真，如果有机会还应该处罚他们，给自己枯燥的生活增添一些乐趣。这一天正是数学老师情绪低落的一天，他对班上的同学说：“今天给你们出一道题，算出1～100这些自然数的和，谁算不出来不许回家吃午饭。”老师讲完这句话后就拿起一本小说坐在椅子上看起来。教室里的小朋友们拿起石板开始计算：“1加2等于3，3加3等于6，6加4等于10……”一些小朋友加到一个数后就擦掉石板上的结果，再加下去，数越来越大，很不好算。
不一会儿，高斯就拿起了他的石板走上前去。“老师，答案是不是这样？”老师头也不抬，说：“去，回去再算！错了。”他认为学生不可能这么快就算出答案的。可是高斯却站着不动，把石板伸到老师面前：“老师！我想这个答案是对的。”数学老师本来想怒斥他，可是一看到石板上整整齐齐地写着5050，他震惊了，因为他自己曾经算过，得到的数也是5050。
高斯解释他发现的计算方法，这个方法就是古时希腊人和中国人用来计算级数1＋2＋3＋…＋n的方法。
高斯的发现使老师觉得羞愧，觉得自己以前轻视穷人家的孩子是不对的。他以后也认真教起书来，并且还常从城里买些数学书借给高斯看。在他的鼓励下，高斯在数学上做了很多重要的研究。
| 欢迎光临 绿色圃中小学教育网 (http://lspjy.com/) | Powered by Discuz! X3.2 |