绿色圃中小学教育网

标题: 小学数学教研论文关于计数单位的教学思考 [打印本页]

作者: 网站工作室 时间: 2013-3-20 18:28
标题: 小学数学教研论文关于计数单位的教学思考
我们

组织学生进行毕业总复习的时候，有关计数单位的题学生掌握得不够理想，引发了我对小学阶段计数单位内容教学的思考。

一

教学一年级（上册）“认数（二）”。

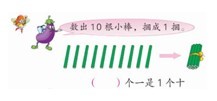
教师提出问题：“摆12根小棒，怎样就能看得很清楚？”有学生摆出了如上图的摆法。教师很满意，正想往下讲，但有一个学生把手举得很高：“这一捆扎得太紧，我数不清。”上课教师一愣，但还算机灵，马上问其他同学：“他的想法你们同意吗？”谁知有不少同学都在点头。

从这个案例中，能看到成人的思维与儿童思维的差异。对具体物品一个一个地数数，一年级的学生并不陌生。但对于整捆的物品，生活中的“整捆”和数学上的“整捆”，是两个完全不同的概念。前者在数量上是随意的，后者刚好是“10”根，多一根少一根都不行。正是由于它的确定性，所以，我们成人眼里看到的整捆不用数也知道是“10”的（限于认识100以内的数时）。

在上这一课之前，学生已基本具备了数数的基础，但是这种数，是基于经验的。我在另外一个班的45人中进行了调查，让他们数出十几根小棒，能数对结果的占总数的95.6%。但学生的数法，全部是把十几根小棒分开，然后一根一根地数。少数特别细心的学生会把小棒摆得很整齐，觉得这样数更方便。由此，就能理解为什么有那么多学生认为“捆得太紧数不清楚”了。

数学知识的学习，是需要基于学生当前经验之后的“数学化”的。苏教版教材特别注意激活学生已有的生活和知识经验，先安排了一根一根地数小棒的活动，再让学生经历将10根小棒捆成一捆的过程，从而帮助学生建立1捆小棒表示10的表象。如图：

对于一年级学生来说，多年来建构的“十几”是松散型的，现在要一下子把松散型的结构调整成两个部分：“十”和“几”，学生往往不明所以。因此，教学中要实实在在地操作，明明白白地讲理，让学生真切地感受如此操作带来的便利，从而在认知过程中逐步“替换”原有的“松散型”结构，并在后续的学习中逐步感悟计数单位。

二

计数单位教学，看似思维难度不大，但我在经历大循环教学之后，发现往往就是因为计数单位建构得不充分，掌握得不扎实，影响了后续的学习。

1.影响数感的培养。

教学苏教版教材二年级（下册）的《认数》单元，在认识三位数后，有一道练习题：738里面有（）个百、（）个十和（）个一，学生都能正确填写。几天之后，我把这道题改成如下形式：738=（）+（）+（），有不少学生就觉得很难，不会填。主要原因是他们仅仅从计算的角度去考虑，认为这题数很大，加的时候很麻烦。个别“聪明”的学生想了很久，终于算出类似的答案738=135+269+334。这一现象，说明学生还不习惯从“百”“十”“个”的计数单位角度去认识一个数，缺少对多位数整体结构的把握。而这一认识上的缺陷，必将影响到更多数位数的认识，进而影响数感的培养。

听五年级（上册）《认识小数》一课时，教师出示了“试一试”中的练习：

这一题的正确答案分数该填“9/1000”，小数该填“0.009”，并联系其他练习认识到“千分之几的分数还可以用三位小数表示”。但当时课堂上教师请的第一个男生说分数时说成了“9/600””，其他学生都不认同。教师意外之余又很耐心地让他说道理，得到的回答是：“正方体有6个面，每个面上有100个小正方体，这样一共是600个小正方体；涂色部分有9个，所以就是9/600”。”听了他的解释后，不少学生又开始点头了。教师为了赶进度，也不敢“恋战”，马上换了一个认为是“9/1000””的学生讲，这个问题就过去了。但一直到下课，刚才认为是9/600”的学生仍然不解地喃喃自语，而有几个同学对他投来同情的目光。这一幕让我印象深刻。

学生在认识一千以内的数时是用一个大正方体表示1000的。“9/600””的出现，说明学生对“千”这一计数单位与其几何直观图的映射关系还没有牢固地建立，这一问题会直接影响对三位小数的认识。

作者: 网站工作室 时间: 2013-3-20 18:28
2.影响对计算算理的理解。
学生在学习分数加法的时候，整数加法的算理无法直接照搬过去，这就引起了学生认知上的冲突。教学异分母分数加法1/2+1/4时，一位教师先让学生尝试，结果有将近一半的学生得到的结果是2/6。而学生讲算理的时候明显受了整数加法的影响，把“相同数位上的数相加”改成了“相同位置上的数相加”，即“分子加分子、分母加分母”。教学的着力点显然是帮助学生理解要把相同的计数单位相加。（分数加法的另一个注意点是化简问题，其中也涉及到计数单位的问题。）
如果对于分数加法算理理解到这个层次，那么对于小数加法要把小数点对齐后相加的道理也就能自然迁移了。这样，整数加法、分数加法、小数加法的计算法则就用“计数单位”统整了，这样的建构将有利于提升学生对加法的认识，促进学生学习能力的提高。
总之，理想的数学教学，应该把一个个散落的知识点按照一定的逻辑关系穿成一条知识链。而认数和计算就要靠“计数单位”这条线去串联。数学教学唯有抓准了这一条条“线”，才能把知识有机进行统整，才能使学生的建构更为科学合理，从而提高学习的效率。

欢迎光临绿色圃中小学教育网 (http://lspjy.com/)