现象二:“这道题没办法求出上底和下底是多少?”
在梯形面积计算的练习中,笔者发现有一道题学生的错误率特别高。这道题是这样的:张大爷用篱笆围一块梯形菜地,一面靠墙(如右图),篱笆全长48米。如果这块地每平方米收白菜9.5千克,一共可以收白菜多少千克?
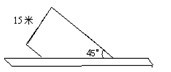
询问学生,学生的回答是:“这道题不能解,因为要求一共可以收白菜多少千克?就要先求出梯形菜地的面积,可是梯形菜地的上底和下底没有办法算出是多少?”
思考及对策:
这是一道难度系数并不高的实际问题,题目不难为何错误率却很高,原因就在于这道题没有像常规问题一样,按部就班分别出示问题所需的条件。学生受常规问题的影响,已经初步形成定势:要求长方形的面积,就要用长乘宽;要求梯形的面积,就要分别知道上底、下底和高。因此条件稍有变化,学生就不知所措了。
要避免这样的现象,首先要注意别让程式化的解题思路固化学生的思维。教学时,不要单纯地训练学生用“要求××,必须要知道××,××已知,××未知,所以我们要先求出××……”表述解题思路。虽说这样的训练能够较好地培养学生的逻辑思维能力,但是如果过分强调,则不利于学生创新思维的发展。要提高学生解决问题的能力,除了让学生掌握一般的思考过程之外,最重要的是让学生深入分析数量关系,根据数量之间的关系确定解题思路。如这样一题:学校开展读书活动,发给3个班图书,每个班发了65本。如果把这些书发给5个班,每班可发多少本?按照常规思路,解决这个问题可以先求出图书总本书,再将图书总本书平均分给5个班,求出每个班发的本书,算式是:65×3÷5。也可先求出65本图书平均分给5个班,每个班可得多少本。然后再乘3算出每个班一共可分得图书多少本。算式是:65÷5×3。要善于从不同的思路加以考虑。再如:

从常规的解题思路来思考,要求花坛的面积只需将1个等腰直角三角形的面积算出,再乘8,算式是:8×8÷2×8。另外我们也可以启发学生作这样的思考,两个等腰直角三角形可以拼成一个正方形,正方形的边长就是等腰直角三角形的腰,因此这题就可以看作是求四个边长是8厘米的正方形的面积之和,算式是8×8÷4。
综上所述,在解决问题的过程中,我们不可满足常规思路,而应该从题中数量关系的特点出发寻求独特的解题思路。这样做并不是为了别具一格,而是为了拓展学生的思维,防止思维的固化。同时,在教学中我们也要注意在练习中及时补充一些变式题,如增加一些无关紧要的条件,改变题中条件的叙述方式,变化条件的呈现顺序,真正培养学生灵活分析数量关系的能力。
现象三:“有两个未知量怎么解?”
六年级的一张测试卷上有这样一题:用一张长82.8厘米的铁皮,剪下一个最大的圆做圆柱的底面,剩下的部分围在底面上做成一个无盖的铁皮水桶。算一算这个铁皮水桶的容积是多少?(铁皮厚度不计)
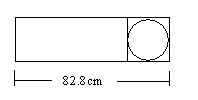
很多学生的第一反应是:只有一个已知条件,怎么解?当教师提示根据图示信息寻找数量之间的关系后,有学生会发现,圆的直径加上圆柱底面周长结果是82.8厘米。应该说,发现这个等量关系后,问题就容易多了。但还是有很多学生没有办法解决,他们的困惑是直径未知,圆柱底面周长还是未知,也就是算术思维定势造成了学生解决问题的困惑。
思考与对策:
学生在六年级时已经学习了ax±bx=c的方程解法,类似数量关系的实际问题学生也基本掌握,那么为何面对这道题,学生束手无策呢?原因主要有:一是题中隐含的条件“d+πd=82.8”学生不容易找到。以前学生接触的是诸如这样的实际问题:地球表面海洋面积大约是陆地面积的2.4倍,比陆地面积多2.1亿平方千米。海洋面积和陆地面积大约各有多少亿平方千米?即两个未知量以明显的倍数关系出现。这时,学生会设单位“1”的量为x,另一个量就用“ax”表示,而这里,尽管两个未知量也是成倍数关系,但是相对比较隐蔽,学生不容易发现。另一个原因笔者认为是算术思维已经深深扎根,学生在解决实际问题遇到困难的时候不容易想到用方程来解决。
针对这样的现象,笔者认为在问题解决教学中,我们要关注两个方面:一方面是要关注数量关系的教学。尽管在教材中没有单独成章的关于数量关系的课时安排,但是不能就此忽视数量关系的教学,要结合具体的情境帮助学生完成数量关系的初步建构,如:速度×时间=路程,单价×数量=总价等。对于数量关系的构建和巩固,要注意通过文字、图示、表格、图文结合等多种方式的问题让学生去接触。学生只有广泛接触不同形式的实际问题,才会不断深化对数量关系的认识和理解。
另一方面,我们要关注代数思维的渗透。学生从一年级学习数学开始,大量接触的是用算术思维思考的实际问题,久而久之,用算术方法解决问题成了他们的思维习惯。为了改变这样的现状,在低年级开始,我们就要注重代数思维的渗透。如低年级起,可以让学生多练习诸如:5+( )=9,7+( )<15的习题;在解决减法实际问题时,不简单否定学生用□+□=□的式子表达计算过程。另外,在学习方程后,教师要有意识地用算术方法和方程作比较,让学生体会到方程解题不仅方便思考(顺向思维),同时也可以沟通不同算法的联系。当学生体会到方程的优越后,就会在解决实际问题的过程中自觉加以运用。
从思维过程的大脑皮层活动情况看,定势是一种习惯性的神经联系,即前次的思维活动对后次的思维活动有指引性的影响。当两次思维活动属于同类性质时,前次思维活动会对后次思维活动起正确的引导作用;当两次思维活动属于异类性质时,前次思维活动会对后次思维活动起错误的引导作用。教学时,我们要避免思维定势造成的负面影响,要注意“活”,强调“变”,注重“新”,培养学生的发散性思维,使学生能够灵活运用所学知识和方法解决实际问题。